biết rằng 2(x+3)2-(2x-3)2= ax2+bx+c. giá trị của biểu thức a+2ab+3c là
A.17
B.73
C.24
D.10
Những câu hỏi liên quan
Biết rằng đồ thị hàm số
y
f
x
x
3
+
a
x
2
+
b
x
+
c
có hai điểm cực trị là A, B và đường thẳng AB đi qua điểm...
Đọc tiếp
Biết rằng đồ thị hàm số y = f x = x 3 + a x 2 + b x + c có hai điểm cực trị là A, B và đường thẳng AB đi qua điểm I 0 ; 1 . Tìm giá trị nhỏ nhất của biểu thức P = a b c + 2 a b + 3 c
A. -22
B. 22
C. -34
D. 34
Chọn đáp án A
Phương trình đường thẳng đi qua hai điểm cực trị là
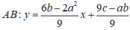
Vì I 0 ; 1 ∈ A B
Khi đó P = a b c + 2 a b + 3 c = 9 c 2 + 12 c - 18
⇒ P = 3 c + 2 2 - 22 ≥ - 22
Dấu “=” xảy ra ⇔ c = - 2 3
Đúng 0
Bình luận (0)
Biết đồ thị hàm số
y
x
+
a
x
2
+
b
x
+
c
có hai điểm cực trị
M
x
1
;
y
1
;
N
x
2
;
y...
Đọc tiếp
Biết đồ thị hàm số y = x + a x 2 + b x + c có hai điểm cực trị M x 1 ; y 1 ; N x 2 ; y 2 thỏa mãn x 1 y 1 - y 2 = y 1 x 1 - x 2 . Giá trị nhỏ nhất của biểu thức abc+2ab+3c bằng
A. - 49 4
B. - 25 4
C. - 841 36
D. - 7 6
Biết đồ thị hàm số
y
x
3
+
a
x
2
+
b
x
+
c
có hai điểm cực trị
M
x
1
;...
Đọc tiếp
Biết đồ thị hàm số y = x 3 + a x 2 + b x + c có hai điểm cực trị M x 1 ; y 1 ; N x 2 ; y 2 thỏa mãn x 1 y 1 - y 2 = y 1 x 1 - x 2 . Giá trị nhỏ nhất của biểu thức a b c + 2 a b + 3 c bằng
A. - 49 4
B. - 25 4
C. - 841 36
D. - 7 6
Chọn đáp án A.
Vì M x 1 ; y 1 , N x 2 ; y 2 là các điểm cực trị của đồ thị hàm số nên y ' x 1 = y ' x 2 = 0
do đó x 1 , x 2 là hai nghiệm phân biệt của y ' = 3 x 2 + 2 a x + b = 0
Ta có phân tích: x 3 + a x 2 + b x + c
Do đó y 1 = 2 3 b - a 2 3 x 1 + c - a b 9
y 2 = 2 3 b - a 2 3 x 2 + c - a b 9
Vì 3 x 1 2 + 2 a x 1 + b = 0 ; 3 x 2 2 + 2 a x 2 + b = 0
Vậy điều kiện bài toán tương đương với
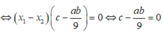
⇔ a b = 9 c
Khi đó:
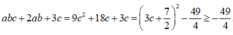
Dấu bằng đạt tại c = - 7 6 ; a b = - 21 2
Đúng 0
Bình luận (0)
6 tháng 9 2021 lúc 13:09
Biết rằng parabol (P): y=ax2+bx+c qua điểm A(3;-7) và có hoành độ đỉnh bằng 1. Tính giá trị của biểu thức 2a+b
Giả sử hàm số f(x) (ax2 + bx + c).e–x là một nguyên hàm của hàm số g(x) x(1 – x).e–x. Giá trị của biểu thức A a + 2b + 3c bằng A. 6 B. 4 C. 9 D. 3
Đọc tiếp
Giả sử hàm số f(x) = (ax2 + bx + c).e–x là một nguyên hàm của hàm số g(x) = x(1 – x).e–x. Giá trị của biểu thức A = a + 2b + 3c bằng
A. 6
B. 4
C. 9
D. 3
Cho hàm số y=f(x) = ax2+ bx+c. Biểu thức f(x+ 3) -3f( x+ 2) +3f( x+ 1) có giá trị bằng.
A. ax2-bx-c.
B. ax2+ bx-c.
C. ax2- bx+ c.
D. ax2+ bx+c.
Ta có:
f(x+3) = a(x+3)2+ b(x+3) +c=ax2+ (6a+b) x+ 9a+ 3b+c
f(x+2) = a(x+2)2+ b(x+2) +c=ax2+ (4a+b) x+ 4a+ 2b+c
f (x+1) = a(x+1)2+ b(x+1) +c=ax2+ (2a+b) x+ 2a+ 2b+c
Suy ra: (x+ 3) -3f( x+ 2) +3f( x+ 1)= ax2+ bx+ c
Chọn D.
Đúng 0
Bình luận (0)
): Cho đa thức f(x) = ax2 + bx + c.
Tính giá trị f(2) biết rằng 4a+c = -2b+2022
\(f\left(2\right)=4a+2b+c\)
Mà \(4a+c=-2b+2022\Rightarrow4a+2b+c=2022\)
Vậy \(f\left(2\right)=2022\)
Đúng 2
Bình luận (0)
\(f\left(2\right)=a2^2+2b+c=4a+2b+c\)
mà \(4a+c=-2b+2022\)
\(\Rightarrow4a+c+2b=2022\)
\(4a+2b+c=2022\)
hay f(2) = 2022
Đúng 0
Bình luận (0)
Giả sử hàm số
f
x
a
x
2
+
b
x
+
c
.
e
-
x
là một nguyên hàm của hàm số
g
x
x
1
-
x...
Đọc tiếp
Giả sử hàm số f x = a x 2 + b x + c . e - x là một nguyên hàm của hàm số g x = x 1 - x . e - x . Giá trị của biểu thức A = a + 2 b + 3 c bằng
A. 6
B. 4
C. 9
D. 3
Cho biểu thức A=(\(\dfrac{x^2}{x^3-4x}+\dfrac{6}{6-3x}+\dfrac{1}{x+2}\)):(x-2 + \(\dfrac{10-x^2}{x+2}\))
a)Rút gọn A
b)Tính giá trị x của A với giá trị của x thỏa mãn |2x-1|=3
c) Tìm x để (3-4x).A<3
d) Tìm giá trị nhỏ nhất của biểu thức B=(8-\(^{x^3}\)).A+x