Một hộp có 5 bi đen, 4 bi trắng. Chọn ngẫu nhiên 2 bi. Xác suất 2 bi được chọn có cùng màu là
A. 1 4
B. 1 9
C. 4 9
D. 5 9
Những câu hỏi liên quan
Một hộp có 5 bi đen, 4 bi trắng. Chọn ngẫu nhiên 2 bi. Xác suất 2 bi được chọn có cùng màu là: A. B. C. D.
Đọc tiếp
Một hộp có 5 bi đen, 4 bi trắng. Chọn ngẫu nhiên 2 bi. Xác suất 2 bi được chọn có cùng màu là:
A. 
B. 
C. 
D. 
Đáp án C
Xác suất 2 bi được chọn có cùng màu là: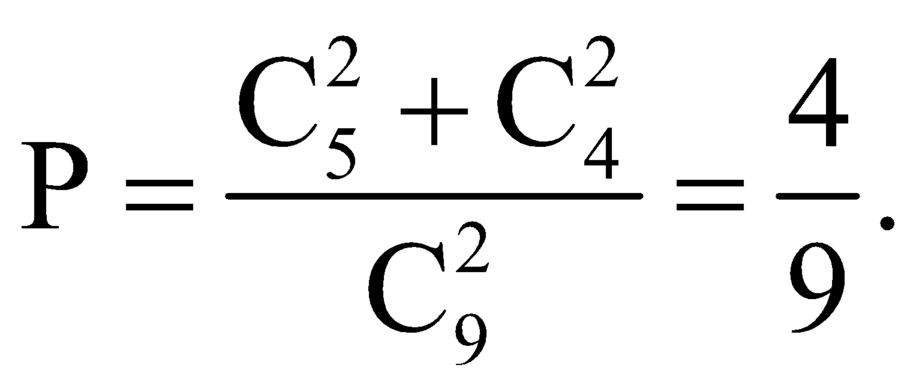 
Đúng 0
Bình luận (0)
Một hộp có 5 bi đen, 4 bi trắng. Chọn ngẫu nhiên 2 bi. Xác suất 2 bi được chọn có cùng màu là:
A. 1 4
B. 1 9
C. 4 9
D. 5 9
Đáp án C
Xác suất 2 bi được chọn có cùng màu là:
Đúng 0
Bình luận (0)
Một hộp có 5 bi đen, 4 bi trắng. Chọn ngẫu nhiên 2 bi. Xác suất 2 bi được chọn có cùng màu là A.
1
4
B.
1
9
C.
4
9
D.
5
9
Đọc tiếp
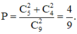
Một hộp có 5 bi đen, 4 bi trắng. Chọn ngẫu nhiên 2 bi. Xác suất 2 bi được chọn có cùng màu là
A. 1 4
B. 1 9
C. 4 9
D. 5 9
Đáp án D
Xác suất 2 bi được chọn có cùng màu là
Đúng 0
Bình luận (0)
Một hộp có 5 bi đỏ, 4 bi trắng. Chọn ngẫu nhiên 2 bi. Xác suất để 2 bi được chọn có đủ hai màu là A.
5
324
B.
2
9
C.
5
9
D.
1
18
Đọc tiếp
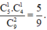
Một hộp có 5 bi đỏ, 4 bi trắng. Chọn ngẫu nhiên 2 bi. Xác suất để 2 bi được chọn có đủ hai màu là
A. 5 324
B. 2 9
C. 5 9
D. 1 18
Một chiếc hộp đựng 7 viên bi màu xanh, 6 viên bi màu đen, 5 viên bi màu đỏ, 4 viên bi màu trắng. chọn ngẫu nhiên ra 4 viên bi, tính xác suất để lấy được ít nhất 2 viên bi cùng màu.
Một hộp đựng 5 bi đỏ, 2 bi đen, và 4 bi trắng. Lấy ngẫu nhiên 2 bi từ trong hộp. a) Tính xác suất để được 2 bi khác màu b) Tính xác suất để được ít nhất 1 bi đỏ
Không gian mẫu: \(C_{11}^2\)
a. Số cách lấy ra 2 viên cùng màu:
\(C_5^2+C_2^2+C_4^2\)
Số cách lấy ra 2 viên khác màu: \(C_{11}^2-\left(C_5^2+C_2^2+C_4^2\right)\)
Xác suất: \(P=\dfrac{C_{11}^2-\left(C_5^2+C_2^2+C_4^2\right)}{C_{11}^2}=...\)
b. Số cách lấy ra 2 viên không có bi đỏ nào: \(C_6^2\)
Số cách lấy ra ít nhất 1 bi đỏ: \(C_{11}^2-C_6^2\)
Xác suất: \(P=\dfrac{C_{11}^2-C_6^2}{C_{11}^2}=...\)
Đúng 2
Bình luận (0)
Một chiếc hộp đựng 7 viên bi màu xanh, 6 viên bị màu đen, 5 viên bị màu đỏ, 4 viên bi màu trắng. Chọn ngẫu nhiên ra 4 viên bị, tính xác suất để lấy được ít nhất 2 viên bị cùng màu.
Một hộp đựng 4 viên bi đỏ, 3 viên bi đen và 2 viên bi trắng. Chọn ngẫu nhiên 2 viên bi. Xác suất để chọn được 2 viên bi khác nhau là A.
5
18
.
B.
13
18
.
C.
13
36
.
D.
10
36
.
Đọc tiếp
Một hộp đựng 4 viên bi đỏ, 3 viên bi đen và 2 viên bi trắng. Chọn ngẫu nhiên 2 viên bi. Xác suất để chọn được 2 viên bi khác nhau là
A. 5 18 .
B. 13 18 .
C. 13 36 .
D. 10 36 .
có 2 hộp đựng bi. Hộp 1 có 7bi xanh, 6 bi đen, hộp 2 có 5bi xanh và 8 bi đen. Chọn ngẫu nhiên 4bi ( mỗi hộp 2 viên). Tính xác suất để lấy được hai viên cùng màu.
\(n\left(\Omega\right)=C^2_{13}\cdot C^2_{13}\)
\(n\left(A\right)=C^2_7\cdot C^2_{13}+C^2_6\cdot C^2_{13}+C^2_5\cdot C^2_{13}+C^2_8\cdot C^2_{13}\)
=>P(A)=5772/6084=37/39
Đúng 0
Bình luận (0)