Với giá trị nào của m thì : Phương trình m x 2 – x – 5 m 2 = 0 có một nghiệm x = -2

Những câu hỏi liên quan
cho hệ phương trình x-y+m=0 và (x+y-2)(x-2y+1) với giá trị nào của m thì hệ phương trình có một nghiệm duy nhất
Cho phương trình x 2 + 2(m + 5)x + 6m - 30 = 0.
a) Với giá trị nào của m thì phương trình có 2 nghiệm phân biệt
x 2 + 2(m + 5)x + 6m - 30 = 0
a) Δ' = b ' 2 - ac = m + 5 2 - (6m - 30)
= m 2 + 10m + 25 - 6m + 30 = m 2 + 4m + 55
= m 2 + 4m + 4 + 51 = m + 2 2 + 51 > 0 ∀m
Vậy phương trình đã cho luôn có 2 nghiệm phân biệt với mọi m
Đúng 0
Bình luận (0)
Với giá trị nào của m thì : Phương trình 2 x 2 – m 2 x +18m = 0 có một nghiệm x = -3
Thay x=-3 vào phương trình 2 x 2 – m 2 x +18m =0 ta được:
2 - 3 2 - m 2 (-3) + 18m =0 ⇔ 3 m 2 +18m+18 =0
⇔ m 2 + 6m +6 = 0 (có hệ số a = 1, b = 6 nên b’ = 3; c = 6)
∆ ' = 3 2 -1.6 = 9 -6 =3 > 0
∆ ' = 3
Phương trình có 2 nghiệm phân biệt:
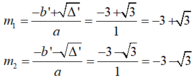
Vậy với m = -3 + 3 hoặc m = -3 - 3 thì phương trình đã cho có nghiệm x = -3
Đúng 0
Bình luận (0)
Cho phương trình (ẩn x) x2 – 2(m – 1)x + m2 = 0
Với giá trị nào của m thì phương trình có hai nghiệm phân biệt? Có nghiệm kép? Vô nghiệm.
Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > 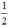
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m = 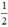
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m < 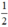
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < 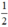 ; có nghiệm kép khi m =
; có nghiệm kép khi m = 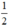 và vô nghiệm khi m >
và vô nghiệm khi m > 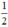
Đúng 0
Bình luận (0)
Cho phương trình:\(x^{2-}\left(m+5\right).x-m+6=0\)(1),( x là ẩn,m là tham số)
a.Giải phương trình với m=1
b.Với giá trị nào của m thì phương trình (1) có 2 nghiệm x1,x2 thỏa mãn:
\(x_1^2+x_1x_2^2=24\)
a) Thay m=1 vào phương trình, ta được:
\(x^2-6\cdot x+5=0\)
a=1; b=-6; c=5
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{5}{1}=5\)
b) Ta có: \(x^2-\left(m+5\right)x-m+6=0\)
a=1; b=-m-5; c=-m+6
\(\Delta=b^2-4ac\)
\(=\left(-m-5\right)^2-4\cdot1\cdot\left(-m+6\right)\)
\(=\left(m+5\right)^2-4\left(-m+6\right)\)
\(=m^2+10m+25+4m-24\)
\(=m^2+14m+1\)
\(=m^2+14m+49-48\)
\(=\left(m+7\right)^2-48\)
Để phương trình có hai nghiệm phân biệt thì \(\left(m+7\right)^2\ge48\)
\(\Leftrightarrow\left[{}\begin{matrix}m+7\ge4\sqrt{3}\\m+7\le-4\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m\ge4\sqrt{3}-7\\m\le-4\sqrt{3}-7\end{matrix}\right.\)
Vì x1,x2 là hai nghiệm của phương trình (1) nên ta có:
\(\left\{{}\begin{matrix}x_1^2-\left(m+5\right)x_1-m+6=0\\x_2^2-\left(m+5\right)x_2-m+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1^2=\left(m+5\right)x_1+m-6\\x_2^2=\left(m+5\right)x_2+m-6\end{matrix}\right.\)
Ta có: \(x_1^2+x_1\cdot x_2^2=24\)
\(\Leftrightarrow\left(m+5\right)x_1+m-6+x_1\cdot\left[\left(m+5\right)x_2+m-6\right]=24\)
\(\Leftrightarrow\left(m+5\right)x_1+m-6+\left(m+5\right)\cdot x_1x_2+x_1\left(m-6\right)=24\)
Xin lỗi bạn, đến đây mình thua
Đúng 0
Bình luận (1)
a, khi m=1
\(=>x^2-6x+5=0\)
\(=>a+b+c=0=>\left[{}\begin{matrix}x1=1\\x2=5\end{matrix}\right.\)
b,\(\Delta=\left[-\left(m+5\right)\right]^2-4\left(-m+6\right)=m^2+10m+25+4m-24\)
\(=m^2+14m+1=m^2+2.7m+49-48\)\(=\left(m+7\right)^2-48\)
pt (1) có nghiệm \(< =>\left(m+7\right)^2-48\ge0\)
\(< =>\left[{}\begin{matrix}m\ge-7+4\sqrt{3}\\m\le-7-4\sqrt{3}\end{matrix}\right.\)
theo vi ét \(=>\left\{{}\begin{matrix}x1+x2=m+5\\x1x2=-m+6\end{matrix}\right.\)
tui nghĩ là đề thế này \(x1^2x2+x1x2^2=24=>x1x2\left(x1+x2\right)=24\)
\(=>\left(6-m\right)\left(m+5\right)=24\)
\(< =>-m^2-5m+6m+30-24=0\)
\(< =>-m^2+m+6=0\)
\(\Delta=1^2-4\left(-1\right).6=25>0\)
\(=>\left[{}\begin{matrix}m1=\dfrac{-1+\sqrt{25}}{2\left(-1\right)}=-2\left(loai\right)\\m2=\dfrac{-1-\sqrt{25}}{2\left(-1\right)}=3\left(tm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho phương trình 7x2 + 2(m – 1)x - m2 = 0.
Với giá trị nào của m thì phương trình có nghiệm?
Ta có: a = 7, b= 2(m-1), c = - m2
Suy ra: Δ' = (m - 1)2 + 7m2
Do (m-1)2 ≥ 0 mọi m và m2 ≥ 0 mọi m
=> ∆’≥ 0 với mọi giá trị của m.
Do đó phương trình có nghiệm với mọi giá trị của m.
Đúng 0
Bình luận (0)
Với giá trị nào m của thì phương trình có nghiệm kép:
\(x^2+\left(3-m\right)x-m-1=0\)
\(\text{Δ}=\left(3-m\right)^2-4\left(-m-1\right)\)
\(=m^2-6m+9+4m+4=m^2-2m+13\)
\(=\left(m-1\right)^2+12>0\)
Vậy: Phương trình không thể có nghiệm kép
Đúng 1
Bình luận (0)
Cho phương trình: x2 - 2(m -1)x + m -5 = 0 với m là tham số
Gọi \(x_1\), \(x_2\) là hai nghiệm của phương trình trên. Với giá trị nào của m thì biểu thức A = \(x^2_1\) + \(x^2_2\) đạt giá trị nhỏ nhất. Tìm giá trị đó
\(\text{Δ}=\left(2m-2\right)^2-4\left(m-5\right)\)
=4m^2-8m+4-4m+20
=4m^2-12m+24
=4m^2-12m+9+15
=(2m-3)^2+15>0
=>PT luôn có hai nghiệm
A=(x1+x2)^2-2x1x2
=(2m-2)^2-2(m-5)
=4m^2-8m+4-2m+10
=4m^2-10m+14
=4(m^2-5/2m+7/2)
=4(m^2-2*m*5/4+25/16+31/16)
=4(m-5/4)^2+31/4>=31/4
Dấu = xảy ra khi m=5/4
Đúng 1
Bình luận (1)
1.Cho phương trình: x2 - 2(m - 2)x + m2 -3m +5 0a) Giải phương trình với m -2b) Tìm các giá trị của m để phương trình có một trong các nghiệm bằng -1c) Tìm các giá trị của m để phương trình trên có nghiệm kép2.Xác định m để mỗi cặp phương trình sau có nghiệm chunga) x2 + mx +2 0 và x2 +2x + m 0b) x2 - (m+4)x + m +5 0 và x2 - (m+2)x +m +1 03. Cho phương trình (m+1)x2 +4mx +4m - 1 0a) Giải phương trình với m - 2b) Với giá trị nào của m thì phương trình có hai nghiệm phân biệtc) Tìm m để phươ...
Đọc tiếp
1.Cho phương trình: x2 - 2(m - 2)x + m2 -3m +5 = 0
a) Giải phương trình với m = -2
b) Tìm các giá trị của m để phương trình có một trong các nghiệm bằng -1
c) Tìm các giá trị của m để phương trình trên có nghiệm kép
2.Xác định m để mỗi cặp phương trình sau có nghiệm chung
a) x2 + mx +2 = 0 và x2 +2x + m = 0
b) x2 - (m+4)x + m +5 =0 và x2 - (m+2)x +m +1 = 0
3. Cho phương trình (m+1)x2 +4mx +4m - 1 =0
a) Giải phương trình với m = - 2
b) Với giá trị nào của m thì phương trình có hai nghiệm phân biệt
c) Tìm m để phương trình có hai nghiệm thỏa mãn điều kiện x1 = - 2x2
4. Cho phương trình x2 - 2(m+4)x +m2 -8 =0
a) Tìm m để biểu thức A= x12 + x22 - x1 - x2 đạt giá trị nhỏ nhất
b) Tìm m để biểu thức B= x1 + x2 -3x1x2 đạt giá trị lớn nhất
c) Tìm m để biểu thức C= x12 + x22 - x1x2 đạt giá trị lớn nhất
Mong mọi người giúp mình, mình thực sự rất cần. Cảm ơn trước ạ. Làm được bài nào thì cmt ngay giúp mình ạ.
Bài 1 : a, Thay m = -2 vào phương trình ta được :
\(x^2+8x+4+6+5=0\Leftrightarrow x^2+8x+15=0\)
Ta có : \(\Delta=64-60=4>0\)
Vậy phương trình có 2 nghiệm phân biệt
\(x_1=\frac{-8-2}{2}=-5;x_2=\frac{-8+2}{2}=-3\)
b, Đặt \(f\left(x\right)=x^2-2\left(m-2\right)x+m^2-3m+5=0\)
\(f\left(-1\right)=\left(-1\right)^2-2\left(m-2\right)\left(-1\right)+m^2-3m+5=0\)
\(1+2\left(m-2\right)+m^2-3m+5=0\)
\(6+2m-4+m^2-3m=0\)
\(2-m+m^2=0\)( giải delta nhé )
\(\Delta=\left(-1\right)^2-4.2=1-8< 0\)
Vậy phương trình vô nghiệm
c, Để phương trình có nghiệm kép \(\Delta=0\)( tự giải :v )












