Với giá trị nào của m thì các phương trình sau có 2 nghiệm phân biệt x 2 – 2(m+3)x + m 2 + 3 = 0

Những câu hỏi liên quan
Câu 25:Với giá trị nào của m thì phương trình: mx^2+2(m-2)x+m-3=0 có 2 nghiệm phân biệt?
Câu 25: \(ĐK:m\ne0\)
PT có 2 nghiệm pb
\(\Leftrightarrow\Delta=4\left(m-2\right)^2-4m\left(m-3\right)>0\\ \Leftrightarrow4m^2-16m+16-4m^2+12m>0\\ \Leftrightarrow16-4m>0\Leftrightarrow m< 4\)
Vậy \(m< 4;m\ne0\)
Đúng 1
Bình luận (0)
Cho phương trình x^2 - 2(m-1)+m^2 Với giá trị nào của m thì phương trình có 2 nghiệm phân biệt Giúp e vs mn :(((
PT có 2 nghiệm phân biệt `<=> '\Delta' >0`
`<=> (m-1)^2-m^2>0`
`<=> m^2-2m+1-m^2>0`
`<=> m < 1/2`
Vậy...
Đúng 1
Bình luận (0)
Cho phương trình
m
x
2
–
2
(
m
–
1
)
x
+
m
–
3
0
. Với giá trị nào dưới đây của m thì phương trình không có hai nghiệm phân biệt A.
m
−
5
4
B.
m
1
4
C.
m
5...
Đọc tiếp
Cho phương trình m x 2 – 2 ( m – 1 ) x + m – 3 = 0 . Với giá trị nào dưới đây của m thì phương trình không có hai nghiệm phân biệt
A. m = − 5 4
B. m = 1 4
C. m = 5 4
D. m = − 1 4
Phương trình mx2 – 2(m – 1)x + m – 3 = 0
có a = m; b’ = − (m – 1); c = m – 3
Suy ra = [− (m – 1)]2 – m(m − 3) = m + 1
Để phương trình có hai nghiệm phân biệt thì
a ≠ 0 Δ ' > 0 ⇔ m ≠ 0 m + 1 > 0 ⇔ m ≠ 0 m > − 1
Nên với đáp án A: m = − 5 4 < − 1
thì phương trình không có hai nghiệm phân biệt
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho phương trình x^2+4mx+4m-1=0
a giải phương trình với m=-2
b với giá trị nào của m thì phương trình có 2 nghiệm phân biệt
a: Khi m=-2 thì phương trình sẽ là \(x^2-8x-9=0\)
=>(x-9)(x+1)=0
=>x=9 hoặc x=-1
b: \(\text{Δ}=\left(4m\right)^2-4\left(4m-1\right)\)
\(=16m^2-16m+4=\left(4m-2\right)^2>=0\)
Để phương trình có hai nghiệm phân biệt thì 4m-2<>0
hay m<>1/2
Đúng 2
Bình luận (0)
`a)` Thay `m=-2` vào ptr có:
`x^2+4.(-2)x+4.(-2)-1=0`
`<=>x^2-8x-9=0`
Ptr có: `a-b+c=1-(-8)+(-9)=0`
`=>x_1=-1;x_2=[-c]/a=9`
Vậy với `m=-2` thì `S={-1;9}`
_____________________________________________
`b)` Ptr có `2` nghiệm pb
`<=>\Delta' > 0`
`<=>(2m)^2-(4m-1) > 0`
`<=>4m^2-4m+1 > 0`
`<=>(2m-1)^2 > 0`
`=>(2m-1)^2 \ne 0`
`<=>2m-1 \ne 0<=>m \ne 1/2`
Vậy ...........
Đúng 1
Bình luận (0)
a) Với m=-2, phương trình đã cho trở thành x2-8x-9=0. Do 1-(-8)+(-9)=0 nên phương trình có hai nghiệm x1=-1 và x2=9.
b) Để phương trình đã cho có hai nghiệm phân biệt thì \(\Delta\)'=(2m)2-(4m-1)>0, suy ra x\(\ne\dfrac{1}{2}\).
Đúng 0
Bình luận (0)
Cho phương trình (ẩn x) x2 – 2(m – 1)x + m2 = 0
Với giá trị nào của m thì phương trình có hai nghiệm phân biệt? Có nghiệm kép? Vô nghiệm.
Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > 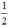
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m = 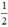
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m < 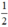
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < 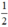 ; có nghiệm kép khi m =
; có nghiệm kép khi m = 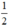 và vô nghiệm khi m >
và vô nghiệm khi m > 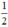
Đúng 0
Bình luận (0)
Cho phương trình x 2 + 2(m + 5)x + 6m - 30 = 0.
a) Với giá trị nào của m thì phương trình có 2 nghiệm phân biệt
x 2 + 2(m + 5)x + 6m - 30 = 0
a) Δ' = b ' 2 - ac = m + 5 2 - (6m - 30)
= m 2 + 10m + 25 - 6m + 30 = m 2 + 4m + 55
= m 2 + 4m + 4 + 51 = m + 2 2 + 51 > 0 ∀m
Vậy phương trình đã cho luôn có 2 nghiệm phân biệt với mọi m
Đúng 0
Bình luận (0)
Cho phương trình x^2-2(m+3)x+m^2-1=0
a)Với giá trị nào của m thì phương trình có hai nghiệm phân biệt.
b)Tìm m để phương trình có 2 nghiệm x1,x2 thỏa mãn (x1+x2)^2-x1.x2+97
Giá trị nào của m thì phương trình (m -3)x^2 +(m +3)x -(m +1) = 0 (1) có hai nghiệm dương phân biệt?
TH1: m=3
Pt sẽ là (3+3)x-(3+1)=0
=>6x-4=0
=>x=2/3
=>Loại
TH2: m<>3
Δ=(m+3)^2-4(m-3)(-m-1)
=m^2+6m+9+4(m-3)(m+1)
=m^2+6m+9+4(m^2-2m-3)
=5m^2-2m-3
Để phương trình có hai nghiệm dương phân biệt thì
5m^2-2m-3>0 và (-m-3)/(m-3)>0 và (-m-1)/(m-3)>0
=>(m-1)(5m+3)>0 và (m+3)/(m-3)<0 và (m+1)/(m-3)<0
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}m>1\\m< -\dfrac{3}{5}\end{matrix}\right.\\-3< m< 3\\-1< m< 3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-1< m< -\dfrac{3}{5}\\1< m< 3\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho phương trình x2 – 2(m – 1)x + 2m – 5 = 0 (m là tham số)
1/ Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi m
2/ Tìm các giá trị của m để phương trình có hai nghiệm trái dậu
3/ Với giá trị nào của m thì biểu thức A = x12 + x22 đạt giá trị nhỏ nhất. Tìm giá trị đó
a/ Xét pt :
\(x^2-2\left(m-1\right)+2m-5=0\)
\(\Delta'=\left(m-1\right)^2-\left(2m-5\right)=m^2-2m+1-2m+5=m^2-4m+6=\left(m-2\right)^2+2>0\forall m\)
\(\Leftrightarrow\) pt luôn có 2 nghiệm pb với mọi m
b/ Phương trình cớ 2 nghiệm trái dấu
\(\Leftrightarrow2m-5< 0\)
\(\Leftrightarrow m< \dfrac{5}{2}\)
c/ Theo định lí Vi - et ta có :
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1.x_2=2m-5\end{matrix}\right.\)
\(A=x_1^2+x_2^2\)
\(=\left(x_1+x_2\right)^2-2x_1.x_2\)
\(=4\left(m-1\right)^2-2\left(2m-5\right)\)
\(=4m^2-8m+4-4m+10\)
\(=4m^2-12m+14=4\left(m^2-3m+\dfrac{9}{4}\right)+5=4\left(m-\dfrac{3}{2}\right)^2+5\ge5\)
\(A_{min}=5\Leftrightarrow m=\dfrac{3}{2}\)
Đúng 2
Bình luận (0)
1, \(\Delta'=\left(m-1\right)^2-\left(2m-5\right)=m^2-4m+6=\left(m-2\right)^2+2>0\)
Vậy pt luôn có 2 nghiệm pb với mọi m
2, Vì pt có 2 nghiệm trái dấu
\(x_1x_2=\dfrac{c}{a}=2m-5< 0\Leftrightarrow m< \dfrac{5}{2}\)
3, Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=2m-5\end{matrix}\right.\)
\(A=\left(x_1+x_2\right)^2-2x_1x_2=4\left(m-1\right)^2-2\left(2m-5\right)\)
\(=4m^2-12m+14=4m^2-2.2m.3+9+6\)
\(=\left(2m-3\right)^2+6\ge6\forall m\)
Dấu ''='' xảy ra khi m = 3/2
Vậy với m = 3/2 thì A đạt GTNN tại 6
Đúng 4
Bình luận (1)
1: \(\text{Δ}=\left(2m-2\right)^2-4\left(2m-5\right)\)
\(=4m^2-8m+4-8m+20\)
\(=4m^2-16m+24\)
\(=4m^2-16m+16+8\)
\(=\left(2m-4\right)^2+8>0\forall m\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
2: Để phương trình có hai nghiệm trái dấu thì 2m-5<0
hay m<5/2
3: \(A=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(2m-2\right)^2-2\left(2m-5\right)\)
\(=4m^2-8m+4-4m+10\)
\(=4m^2-12m+14\)
\(=4m^2-12m+9+5\)
\(=\left(2m-3\right)^2+5\ge5\forall m\)
Dấu '=' xảy ra khi m=3/2
Đúng 1
Bình luận (0)




















