Đáp án C

Bỏ 4 lá thư vào 4 phong bì ta có số cách bỏ là.

 4! Cách.

Ta xét các trường hợp sau. 

TH1: chỉ có một lá thư bỏ đúng. giải sử ta chọn 1 trong 4 lá để bỏ đúng (có 4 cách), trong mỗi cách đó chọn một lá để bỏ sai (có 2 cách), khi đó 2 lá còn lại nhất thiết là sai (1 cách), vậy trong TH1 này có 4.2.1=8 cách.

TH2: có đúng 2 lá bỏ đúng. Tương tự trên, ta chọn 2 lá bỏ đúng (có 6 cách), 2 lá còn lại nhất thiết sai (1 cách), vậy trong TH2 này có 6 cách.

TH3: dễ thấy khi 3 lá đã bỏ đúng thì đương nhiên là cả 4 lá đều đúng, vậy có 1 cách.

Suy ra có 8+6+1=15 cách bỏ ít nhất có 1 lá thư vào đúng địa chỉ.

Vậy xác suất cần tìm là: 15/24=5/8

Đáp án C

Bỏ 4 lá thư vào 4 phong bì ta có số cách bỏ là. 4! Cách.

Ta xét các trường hợp sau

TH1: chỉ có một lá thư bỏ đúng. giải sử ta chọn 1 trong 4 lá để bỏ đúng (có 4 cách)

trong mỗi cách đó chọn một lá để bỏ sai (có 2 cách), khi đó 2 lá còn lại nhất thiết là sai (1 cách)

vậy trong TH1 này có 4.2.1 = 8 cách.

TH2: có đúng 2 lá bỏ đúng. Tương tự trên, ta chọn 2 lá bỏ đúng (có C 4 2 = 6  cách)

2 lá còn lại nhất thiết sai (1 cách), vậy trong TH2 này có 6 cách.

TH3: dễ thấy khi 3 lá đã bỏ đúng thì đương nhiên là cả 4 lá đều đúng, vậy có 1 cách.

Suy ra có 8+6+1=15 cách bỏ ít nhất có 1 lá thư vào đúng địa chỉ.

Vậy xác suất cần tìm là: 15 24 = 5 8

Đáp án A

Phương pháp giải: Áp dụng nguyên lý bù trừ trong bài toán xác suất

Lời giải:

Ta tính xác suất để xảy ra không một lá thư nào đúng địa chỉ.

Mỗi phong bì có 4 cách bỏ thư vào nên có tất cả 4! cách bỏ thư.

Gọi U là tập hợp các cách bỏ thư và A_m là tính chất lá thư thứ m bỏ đúng địa chỉ.

Khi đó, theo công thức về nguyên lý bù trừ, ta có  N ¯ = 4 ! - N 1 + N 2 - . . . + ( - 1 ) 4 N 4 .

Trong đó N_m ( 1 ≤ m ≤ 4 ) là số tất cả các cách bỏ thư sao cho có m lá thư đúng địa chỉ.

Nhận xét rằng, N_m là tổng theo mọi cách lấy m lá thư từ 4 lá, với mỗi cách lấy m lá thư, có (4 - m)! cách bỏ m lá thư này đúng địa chỉ, ta nhận được:

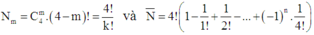
Suy ra xác suất cần tìm cho việc không lá thư nào đúng địa chỉ là

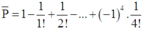
Vậy xác suất để có ít nhất 1 lá thư bỏ đúng phong bì của nó là  P = 1 - P ¯ = 5 8 .

Đáp án A

Phương pháp giải: Áp dụng nguyên lý bù trừ trong bài toán xác suất

Lời giải:

Ta tính xác suất để xảy ra không một lá thư nào đúng địa chỉ.

Mỗi phong bì có 4 cách bỏ thư vào nên có tất cả 4! cách bỏ thư.

Gọi U là tập hợp các cách bò thư và A m  là tính chất lá thư thứ m bỏ đúng địa chỉ.

Khi đó, theo công thức về nguyên lý bù trừ, ta có N ¯ = 4 ! − N 1 + N 2 − ... + − 1 4 N 4  

Trong đó N m 1 ≤ m ≤ 4  là số tất cả các cách bỏ thư sao cho có m lá thư đúng địa chỉ.

Nhận xét rằng, N m  là tổng theo mọi cách lấy m lá thư từ 4 lá, với mỗi cách lấy m lá thư, có 4 − m !  cách bỏ m lá thư này đúng địa chỉ, ta nhận được: N m = C 4 m . 4 − m ! = 4 ! k !  và 

N ¯ = 4 ! 1 − 1 1 ! + 1 2 ! − ... + − 1 n . 1 4 !

Suy ra xác suất cần tìm cho việc không lá thư nào đúng địa chỉ là  P ¯ = 1 − 1 1 ! + 1 2 ! − ... + − 1 4 . 1 4 !

Vậy xác suất để có ít nhất 1 lá thư bỏ đúng phong bì của nó là  P = 1 − P ¯ = 5 8

Số cách bỏ 4 lá thư vào 4 bì thư là: 

Kí hiệu 4 lá thư là: L_1,L_2,L_3,L₄ và bộ (L₁L₂L₃L₄) là một hóan vị của các số 1;2;3;4 trong đó nếu lá thư L_i  bỏ đúng địa chỉ.

 Ta xét các khả năng sau 

 có 4 lá thư bỏ đúng địa chỉ:(1;2;3;4) nên có 1 cách bỏ

 có 2 là thư bỏ đúng địa chỉ:

 +) số cách bỏ 2 lá thư đúng địa chỉ là: 

 +) khi đó có 1 cách bỏ hai là thư còn lại

Nên trường hợp này có:  cách bỏ.

 Có đúng 1 lá thư bỏ đúng địa chỉ:

Số cách chọn lá thư bỏ đúng địa chỉ: 4 cách

Số cách chọn bỏ ba lá thư còn lại:  cách

Nên trường hợp này có:  cách bỏ.

Do đó: 

Vậy .

Chọn A.

Chọn B

Đáp án D

Số phần tử không gian mẫu là:  n ( Ω ) = 3 ! = 6 .

Gọi A là biến cố “Có ít nhất một lá thư được bỏ đúng phong bì”.

Ta xét các trường hợp sau:

Nếu lá thứ nhất bỏ đúng phong bì, hai lá còn lại để sai thì có duy nhất 1 cách.  

Nếu lá thứ hai bỏ đúng phong bì, hai lá còn lại để sai thì có duy nhất 1 cách.

Nếu lá thứ ba bỏ đúng phong bì, hai lá còn lại để sai thì có duy nhất 1 cách.

Không thể có trường hợp hai lá thư bỏ đúng và một lá thư bỏ sai.

Cả ba lá thư đều được bỏ đúng có duy nhất 1 cách.

⇒ n A = 4

Vậy xác suất để có ít nhất một lá thư được bỏ đúng phong bì là:

  P ( A ) = n ( A ) n Ω = 4 6 = 2 3 .

Cách 2:

Gọi B là biến cố “Không có lá thư nào được bỏ đúng phong bì”.

⇒ n B = 2

P ( A ) = 1 - P ( B ) = 1 - n ( B ) n Ω = 1 - 2 6 = 2 3 .

Xét các dãy số x 1 ; x 2 ; x 3 , trong đó x 1 ; x 2 ; x 3 là một hoán vị của ba số 1,2,3 (ở đây x i = i , tức là lá thư i đã bỏ đúng địa chỉ).

Gọi Ω là tập hợp tất cả các khả năng bỏ 3 lá thư vào 3 phong bì. Khi đó Ω = 3 ! = 6 .

Gọi A là biến cố: “Có ít nhât 1 lá thư bỏ đúng phong bì”. Các khả năng thuận lợi của A là ( 1;2;3 ); ( 1;3;2 ); ( 3;2;1 ); ( 2;1;3 ). Do vậy Ω A = 4 .

Từ đó P ( A ) = Ω A Ω = 4 6 = 2 3

Đáp án cần chọn là A

-         Số phần tử của không gian mẫu là: \(n\left( \Omega  \right) = 3! = 6\)

-         Gọi B là biến cố “Không lá thư nào được bỏ đúng phong bì”

A là biến cố “Có ít nhất một lá thư được bỏ đúng phong bì”

⇨     n(B) = 2

⇨     \(P(A) = 1 - P(B) = 1 - \frac{2}{6} = \frac{2}{3}\)