Giup mik cau 31 vs hic

Những câu hỏi liên quan
Giup minh ba cau nay vs hic
cac cau giup mik vs mik dang can gap
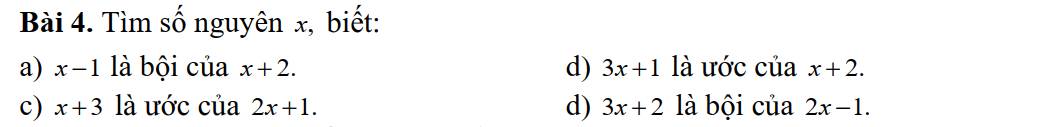
a: x-1 là bội của x+2
=>\(x-1⋮x+2\)
=>\(x+2-3⋮x+2\)
=>\(-3⋮x+2\)
=>\(x+2\inƯ\left(-3\right)\)
=>\(x+2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{-1;-3;1;-5\right\}\)
b: 3x+1 là ước của x+2
=>\(x+2⋮3x+1\)
=>\(3x+6⋮3x+1\)
=>\(3x+1+5⋮3x+1\)
=>\(5⋮3x+1\)
=>\(3x+1\in\left\{1;-1;5;-5\right\}\)
=>\(3x\in\left\{0;-2;4;-6\right\}\)
=>\(x\in\left\{0;-\dfrac{2}{3};\dfrac{4}{3};-2\right\}\)
mà x nguyên
nên \(x\in\left\{0;-2\right\}\)
c: x+3 là ước của 2x+1
=>\(2x+1⋮x+3\)
=>\(2x+6-7⋮x+3\)
=>\(-7⋮x+3\)
=>\(x+3\in\left\{1;-1;7;-7\right\}\)
=>\(x\in\left\{-2;-4;4;-10\right\}\)
d: 3x+2 là bội của 2x-1
=>\(3x+2⋮2x-1\)
=>\(6x+4⋮2x-1\)
=>\(6x-3+7⋮2x-1\)
=>\(7⋮2x-1\)
=>\(2x-1\in\left\{1;-1;7;-7\right\}\)
=>\(2x\in\left\{2;0;8;-6\right\}\)
=>\(x\in\left\{1;0;4;-3\right\}\)
Đúng 1
Bình luận (0)
Giup mik cau 1 vs
Giup mik câu 3 cau 4 vs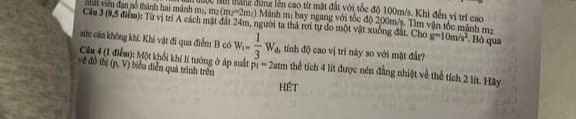
 ai giai giup mik cau 9 , 10 vs aj
ai giai giup mik cau 9 , 10 vs aj
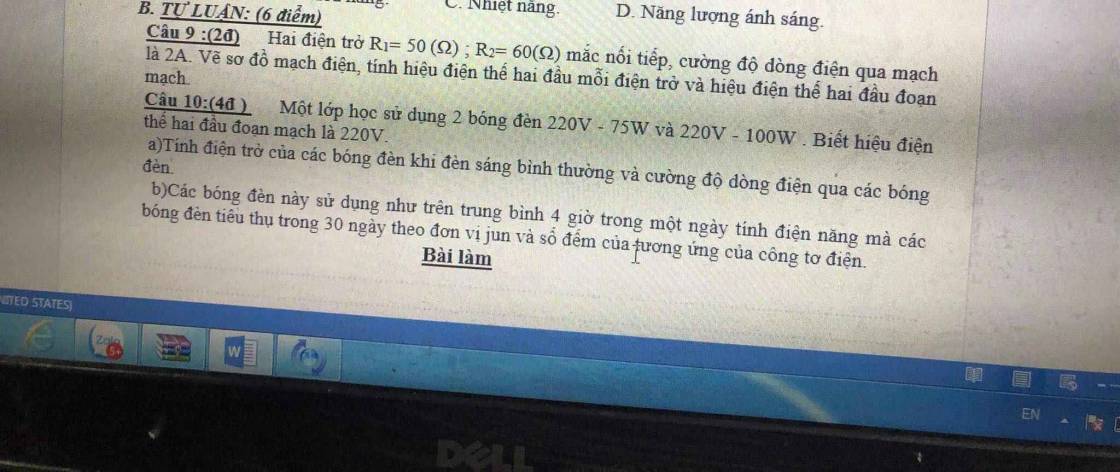
Câu 9.
\(R_1ntR_2\Rightarrow I_1=I_2=I=2A\)
\(R_{tđ}=R_1+R_2=50+60=110\Omega\)
\(U_1=I_1\cdot R_1=2\cdot50=100V\)
\(U_2=I_2\cdot R_2=2\cdot60=120V\)
\(U=U_1+U_2=100+120=220V\)
Câu 10.
a)Khi các đèn sáng bình thường.
\(R_1=\dfrac{U_1^2}{P_1}=\dfrac{220^2}{75}=\dfrac{1936}{3}\Omega;I_{đm1}=\dfrac{P_1}{U_1}=\dfrac{75}{220}=\dfrac{15}{44}A\)
\(R_2=\dfrac{U_2^2}{P_2}=\dfrac{220^2}{100}=484\Omega;I_{đm2}=\dfrac{P_2}{U_2}=\dfrac{100}{220}=\dfrac{5}{11}A\)
Hai bóng đèn mắc song song nên dòng điện qua các bóng đèn là:
\(I_1=\dfrac{U}{R_1}=\dfrac{220}{\dfrac{1936}{3}}=\dfrac{15}{44}A\)
\(I_2=\dfrac{U}{R_2}=\dfrac{220}{484}=\dfrac{5}{11}A\)
b)Điện năng hai bóng đèn tiêu thụ trong một ngày là:
\(A_1=U_1I_1t+U_2I_2t=220\cdot\dfrac{15}{44}\cdot4\cdot3600+220\cdot\dfrac{5}{11}\cdot4\cdot3600=2520000J\)
\(\Rightarrow A_1=0,7kWh\)
Điện năng hai đèn tiêu thụ trong 30 ngày là:
\(A=30\cdot0,7=21kWh\)
Số đếm tương ứng của công tơ điện là 21 số điện.
Đúng 1
Bình luận (0)
giup mik cau 4 cua bai 6 vs a

1: Xet ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
2: ΔABC vuông tại A có AH là đường cao
nên HA^2=HB*HC
3: AC=căn 10^2-6^2=8cm
BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=8/8=1
=>AD=3cm; CD=5cm
4: AH=4,8cm
=>BH=3,6cm; CH=6,4cm
HE=2*AH=9,6
=>\(BE=\dfrac{6\sqrt{73}}{5};CE=\dfrac{16\sqrt{13}}{5}\)
BH*BC=CK*BE
=>\(CK=\dfrac{80\sqrt{73}}{73}\left(cm\right);BK=\dfrac{30\sqrt{73}}{7}\left(cm\right)\)
HC/CK=HM/KB
=>HM=2,4cm=1/2HA
=>ĐPCM
Đúng 0
Bình luận (0)
Mấy ban CTV ơi giup mih cau 30 vs 31 vs
câu 30 y'=0 ta có 3 nghiệm x=0 và x=+-căn(m) vs x=+-căn(m)=>y=-m2 =>A(-căn(m);-m^2).B(căn(m);-m^2)=> kc AB=2 căn(m) tại x=0 y=0 =>O(0;0) vì hàm có 3 cực trị =>tam giác 0AB cân => m^2 là đường cao Soab=(2 căn(m)*m^2)/2 =căn(m)^3<1 gọi căn m là x => x^3-1<0 áp dụng hằng đt => x-1<0 => x<1 =>m<1
Đúng 0
Bình luận (0)
giup mih cau 30 31 vs
Lời giải:
Bài 30:
Ta có \(y=x^4-2mx^2\Rightarrow y'=4x^3-4mx\)
Để ĐTHS có 3 điểm cực trị thì \(y'=4x^3-4mx=0\) phải có ba nghiệm phân biệt
\(\Leftrightarrow x(x^2-m)=0\) có ba nghiệm phân biệt. Do đó \(m>0\)
Khi đó, gọi ba điểm cực trị lần lượt là:
\(A(0,0);B(\sqrt{m},-m^2);C(-\sqrt{m},-m^2)\)
Từ đây, ta viết được PTĐT $BC$ là: \(y=-m^2\)
Sử dụng công thức tính khoảng cách từ 1 điểm đến đường thẳng:
\(d(A,BC)=\frac{|m^2|}{\sqrt{1^2+0^2}}=m^2\)
\(BC=\sqrt{(\sqrt{m}--\sqrt{m})^2+(-m^2+m^2)^2}=2\sqrt{m}\)
\(\Rightarrow S_{ABC}=\frac{d(A,BC).BC}{2}=m^2\sqrt{m}<1\). Mà \(m>0\) nên
\(m^2\sqrt{m}<1\Leftrightarrow 0<\sqrt{m^5}<1\Leftrightarrow 0< m<1\).
Đáp án D.
Đúng 0
Bình luận (0)
Bài 31:
Đề bài sai rồi nhé, hàm thứ hai phải là \(y=x^3-3x^2-m+2\)
PT hoành độ giao điểm:
\(x^3-3x^2-m+2+mx=0\)
\(\Leftrightarrow (x-1)[x^2-2x+(m-2)]=0\)
PT trên có một nghiệm là $1$. Để hai đths cắt nhau tại ba điểm phân biệt thì PT \(x^2-2x+(m-2)=0(1)\) phải có hai nghiệm pb khác $1$
\(\Rightarrow \left\{\begin{matrix} 1-2-2+m\neq 0\\ \Delta'=3-m>0\end{matrix}\right.\Rightarrow m<3\)
Nếu $x_1,x_2$ là hai nghiệm của $(1)$ thì áp dụng định lý Viete ta có:
\(\left\{\begin{matrix} x_1+x_2=2\\ x_1x_2=m-2\end{matrix}\right.\)
Như vậy, độ dài các đoạn $AB,BC,AC$ nằm trong các giá trị:
\(\left\{\begin{matrix} |x_1-1|\sqrt{m^2+1}\\ |x_2-1|\sqrt{m^2+1}\\ |x_1-x_2|\sqrt{m^2+1}\end{matrix}\right.\)
Ta thấy \(x_1+x_2=2\Rightarrow x_1-1=1-x_2\Rightarrow |x_1-1|=|x_2-1|\)
Do đó \(|x_1-1|\sqrt{m^2+1}=|x_2-1|\sqrt{m^2+1}\), tức là luôn tồn tại hai đoạn thẳng nối hai giao điểm có độ dài bằng nhau (thỏa mãn đkđb) , với mọi $m$ nằm trong khoảng xác định, hay \(m<3\)
Đáp án D.
Đúng 0
Bình luận (0)
mn oi giup mik vs 2 cau khoanh tron yy a













