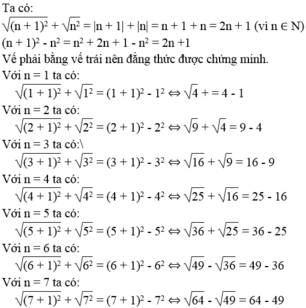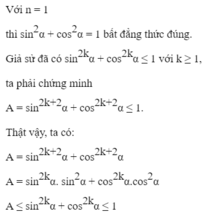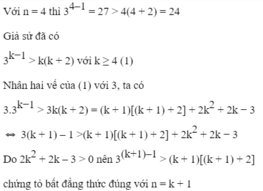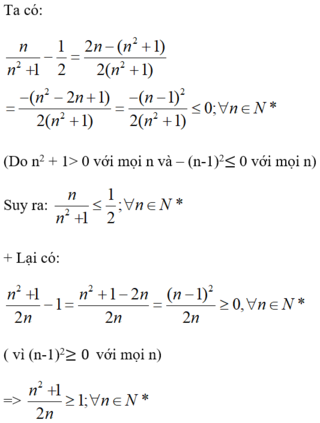Chứng minh đẳng thức: n + 1 - n = 1 n + 1 + n với n là số tự nhiên
Những câu hỏi liên quan
Chứng minh đẳng thức:
1/n(n+1)=1/n-1/n+1
Ta có: \(\dfrac{1}{n\left(n+1\right)}=\dfrac{1}{n}-\dfrac{1}{n+1}\)
Vì \(\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{1}{n}-\dfrac{1}{n+1}\)
\(\Rightarrow\dfrac{1}{n\left(n+1\right)}=\dfrac{1}{n}-\dfrac{1}{n+1}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Chứng minh
\(\dfrac{1}{n\left(n+1\right)}\)=\(\dfrac{1}{n}-\dfrac{1}{n+1}\)
Ta có:VP=\(\dfrac{1}{n}-\dfrac{1}{n+1}\)=
\(\dfrac{n+1}{n\left(n+1\right)}-\dfrac{n}{n\left(n+1\right)}\)
=\(\dfrac{n+1-n}{n\left(n+1\right)}=\dfrac{1}{n\left(n+1\right)}=VT\)(đpcm)
Đúng 0
Bình luận (3)
Với n là số tự nhiên, chứng minh đẳng thức:
n
+
1
2
+
n
2
n
+
1
2...
Đọc tiếp
Với n là số tự nhiên, chứng minh đẳng thức:
n + 1 2 + n 2 = n + 1 2 - n 2
Viết đẳng thức trên khi n là 1, 2, 3, 4, 5, 6, 7
Chứng minh bất đẳng thức Cô-si với n số không âm.
1) chứng minh bất đẳng thức Bu-nhi-a-cốp-ski với bộ n số.
Ai nhanh mình tick!^_^
Chứng minh các bất đẳng thức sau ( n ∈ N ∗ ) sin 2 n α + cos 2 n α ≤ 1 .
Chứng minh các bất đẳng thức sau 3n − 1 > n(n + 2) với n ≥ 4
Chứng minh đẳng thức sau (
v
ớ
i
n
∈
N
∗
)
2
+
5
+
8
+
.
.
.
+
(
3
n
-
1
)
3
3...
Đọc tiếp
Chứng minh đẳng thức sau ( v ớ i n ∈ N ∗ ) 2 + 5 + 8 + . . . + ( 3 n - 1 ) = 3 3 n + 1 2
Đặt vế trái bằng S n . Kiểm tra với n = 1 hệ thức đúng.
Giả sử đã có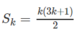 
với k ≥ 1.
Ta phải chứng minh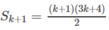 
Thật vậy
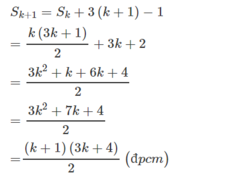
Đúng 0
Bình luận (0)
Với n là số tự nhiên,chứng minh đẳng thức:
\(\sqrt{\left(n+1\right)^2}+\sqrt{n^2}=\left(n+1\right)^2-n^2\)
Viết đẳng thức khi n là 1,2,3,4,5,6,7.
\(\sqrt{\left(n+1\right)^2}+\sqrt{n^2}=\left(n+1\right)+n=2n+1=\left(n+1-n\right)\left(n+1+n\right)=\left(n+1\right)^2-n^2\)
Đúng 0
Bình luận (0)
Chứng minh các bất đẳng thức
n
n
2
+
1
≤
1
2
và
n
2
+
1
2
n...
Đọc tiếp
Chứng minh các bất đẳng thức n n 2 + 1 ≤ 1 2 và n 2 + 1 2 n ≥ 1 với mọi n ∈ N * .
chứng minh đẳng thức : \(\dfrac{1}{n\left(n+1\right)}=\dfrac{1}{n}-\dfrac{1}{n+1}\)
xuất phát từ vế phải và quy đồng mẫu thức, ta có :
VP=\(\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{n+1}{n\left(n+1\right)}-\dfrac{n}{n\left(n+1\right)}=\dfrac{n+1-n}{n\left(n+1\right)}=\dfrac{1}{n\left(n+1\right)}\left(dpcm\right)\)
Đúng 0
Bình luận (0)
\(\dfrac{1}{n\left(n+1\right)}=\dfrac{1}{n}-\dfrac{1}{n+1}\)
<=>\(\dfrac{1}{n\left(n+1\right)}=\dfrac{n+1}{n\left(n+1\right)}-\dfrac{n}{n\left(n+1\right)}\)
<=>1=n+1-n
<=>1=1
vậy \(\dfrac{1}{n\left(n+1\right)}=\dfrac{1}{n}-\dfrac{1}{n+1}\)
Đúng 0
Bình luận (0)