Các câu hỏi tương tự
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
Chứng minh các bất đẳng thức sau 3n − 1 > n(n + 2) với n ≥ 4
Cho góc bất kì α. Chứng minh các đẳng thức sau:
a) (sinα+cosα)2=1+sin2α;
b) cos4α−sin4α=cos2α.
Chứng minh các bất đẳng thức sau ( n ∈ N ∗ ) 2 n + 2 > 2 n + 5
Chứng minh các đẳng thức sau với
n
∈
N
∗
S
n
sin
x
+
sin
2
x
+
.
.
.
+
sin
n
x
sin...
Đọc tiếp
Chứng minh các đẳng thức sau với n ∈ N ∗ S n = sin x + sin 2 x + . . . + sin n x = sin n x 2 . sin n + 1 x 2 sin x 2
Cho góc
α
cho thỏa 0
α
π
4
và sin
α
+ cos
α
5
2
Tính P sin
α
-cos
α
.
Đọc tiếp
Cho góc α cho thỏa 0 < α < π 4 và sin α + cos α = 5 2 Tính P = sin α -cos α .
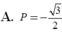
![]()
![]()
![]()
Tìm đạo hàm của hàm số sau: y = ( x . sin α + cos α ) ( x . cos α − sin α )
Chứng minh các bất đẳng thức
n
n
2
+
1
≤
1
2
và
n
2
+
1
2
n...
Đọc tiếp
Chứng minh các bất đẳng thức n n 2 + 1 ≤ 1 2 và n 2 + 1 2 n ≥ 1 với mọi n ∈ N * .