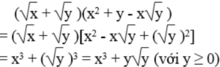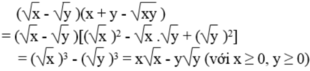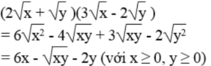Khai triển và rút gọn các biểu thức (với x và y không âm) 4 x - 2 x x - 2 x

Những câu hỏi liên quan
Khai triển và rút gọn các biểu thức (với x và y không âm) x + 2 x - 2 x + 4
Khai triển và rút gọn các biểu thức (với x và y không âm) x + y x 2 + y - x y
Khai triển và rút gọn các biểu thức (với x và y không âm) x - y x + y - x y
Khai triển và rút gọn các biểu thức (với x và y không âm) 1 - x 1 + x + x
Khai triển và rút gọn các biểu thức (với x và y không âm) 2 x + y 3 x - 2 y
Khai triển và rút gọn biểu thức:
\(\left(1-\sqrt{x}\right)\left(1+\sqrt{x}+x\right)\)(với x và y không âm )
\(\left(4\sqrt{x}-\sqrt{2x}\right)\left(\sqrt{x-\sqrt{2x}}\right)\)(với x, y không âm)
a> c1: \(=1-\sqrt{x^3}=1-\sqrt{x^2.x}=1-x\sqrt{x}\)
c2 \(=1+\sqrt{x}+x-\sqrt{x}-x-x\sqrt{x}=1-x\sqrt{x}\)
b> c1: \(=\sqrt{x}\left(4-\sqrt{2}\right)\sqrt{x-\sqrt{2x}=\sqrt{x\left(x-\sqrt{2x}\right)}}\left(4-\sqrt{2}\right)\)
c2: \(=4\sqrt{x\left(x-\sqrt{2x}\right)}-\sqrt{2x\left(x-\sqrt{2x}\right)}=\sqrt{x\left(x-\sqrt{2x}\right)}\left(4-\sqrt{2}\right)\)
Đúng 0
Bình luận (0)
Khai triển và rút gọn các biểu thức (với x, y không âm)
a) \(\left(4\sqrt{x}-\sqrt{2x}\right)\left(\sqrt{x}-\sqrt{2x}\right)\)
b) \(\left(2\sqrt{x}+\sqrt{y}\right)\left(3\sqrt{x}-2\sqrt{y}\right)\)
\(a,\left(4\sqrt{x}-\sqrt{2x}\right)\left(\sqrt{x}-\sqrt{2x}\right)=4x-4\sqrt{2}x-\sqrt{2}x+2x=6x-5\sqrt{2}x=\left(6-5\sqrt{2}\right)x\)
\(b,\left(2\sqrt{x}+\sqrt{y}\right)\left(3\sqrt{x}-2\sqrt{y}\right)=6x-4\sqrt{xy}+3\sqrt{xy}-2y=6x-4\sqrt{xy}-2y\)
Đúng 0
Bình luận (0)
Khai triển và rút gọn các biểu thức (với x và y không âm)
a) (4\(\sqrt{x}\)-\(\sqrt{2x}\))(\(\sqrt{x}\)-\(\sqrt{2x}\))
b) (2\(\sqrt{x}\)+\(\sqrt{y}\))(3\(\sqrt{x}\)-2\(\sqrt{y}\))
a: \(=4x-4x\sqrt{2}-2x\sqrt{2}+2x=6x-6x\sqrt{2}\)
b: \(=6x-4\sqrt{xy}+3\sqrt{xy}-2y=6x-\sqrt{xy}-2y\)
Đúng 0
Bình luận (0)
Khai triển và rút gọn các biểu thức (với x và y không âm)
a) \(\left(1-\sqrt{x}\right)\left(1+\sqrt{x}+x\right)\)
b) \(\left(\sqrt{x}+2\right)\left(x-2\sqrt{x}+4\right)\)
c) \(\left(\sqrt{x}-\sqrt{y}\right)\left(x+y+\sqrt{xy}\right)\)
d) \(\left(x+\sqrt{y}\right)\left(x^2+y-x\sqrt{y}\right)\)
a)\(\left(1-\sqrt{x}\right)\left(1+\sqrt{x}+x\right)=1-\sqrt{x^3}\)
b) \(\left(\sqrt{x}+2\right)\left(x-2\sqrt{x}+4\right)=\sqrt{x^3}+8\)
c)\(\left(\sqrt{x}-\sqrt{y}\right)\left(x+y+\sqrt{xy}\right)=\sqrt{x^3}-\sqrt{y^3}\)
d)\(\left(x+\sqrt{y}\right)\left(x^2+y-x\sqrt{y}\right)=x^3+\sqrt{y^3}\)
Đúng 0
Bình luận (0)