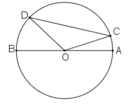
Giả sử ta có đường tròn tâm O đường kính AB, dây CD khác với đường kính

Vì O,C,D không thẳng hàng

nên DC<OC+OD=2R=AB

=>AB là dây lớn nhất

Giả sử ta có đường tròn đường kính AB = 2R và một dây CD.

Trong ΔCOD, theo bất đẳng thức tam giác ta có:

    CD ≤ OC + CD

=> CD ≤ 2R

=> CD ≤ AB (đpcm)

Giả sử ta có đường tròn đường kính AB = 2R và một dây CD. Trong COD, theo bất đẳng thức tam giác ta có:

CD ≤ OC + CD => CD ≤ 2R => CD ≤ AB

* Xét tam giác ACO có CO’ là đường trung tuyến và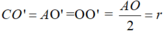 

Suy ra, tam giác ACO vuông tại C

⇒ AC ⊥ CO

* Xét tam giác AOD có AO = OD = R

Suy ra tam giác AOD cân tại O.

Lại có OC là đường cao nên đồng thời là đường trung tuyến

⇒ C là trung điểm AD hay AC = CD. (điều phải chứng minh)

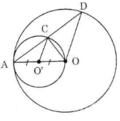
a) Gọi O’ là tâm của đường tròn đường kính OA.

Gọi R và r lần lượt là bán kính đường tròn tâm O và tâm O’.

Suy ra, hai đường tròn đã cho tiếp xúc trong với nhau.

b) +) Xét đường tròn (O’) có A, O, C là ba điểm cùng thuộc đường tròn và OA là đường kính nên tam giác AOC vuông tại C.

⇒ OC ⊥ AD

+) Xét đường tròn tâm (O) có A, D là hai điểm thuộc đường tròn nên OA = OD

⇒ ΔAOD cân tại O mà OC ⊥ AD

⇒ OC là đường trung tuyến của ΔAOD

⇒ C là trung điểm của AD

⇒ AC = CD

Hướng dẫn giải:

a) Gọi O' là tâm của đường tròn đường kính OA thì O'A=O'O.

Ta có OO'=OA-O'A hay d=R-r nên đường tròn (O) và đường tròn (O') tiếp xúc trong.

b) Tam giác CAO có cạnh OA là đường kính của đường tròn ngoại tiếp nên ΔCAO vuông tại C

⇒OC⊥AD

⇒CA=CD (đường kính vuông góc với một dây).