Question

 Cho đường tròn tâm O bán kính OA và đường tròn đường kính OA.

a) Hãy xác định vị trí tương đối của hai đường tròn.

b) Dây AD của đường tròn lớn cắt đường tròn nhỏ ở C. Chứng minh rằng AC = CD.

Answer 1

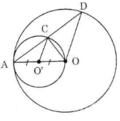
a) Gọi O’ là tâm của đường tròn đường kính OA.

Gọi R và r lần lượt là bán kính đường tròn tâm O và tâm O’.

Suy ra, hai đường tròn đã cho tiếp xúc trong với nhau.

b) +) Xét đường tròn (O’) có A, O, C là ba điểm cùng thuộc đường tròn và OA là đường kính nên tam giác AOC vuông tại C.

⇒ OC ⊥ AD

+) Xét đường tròn tâm (O) có A, D là hai điểm thuộc đường tròn nên OA = OD

⇒ ΔAOD cân tại O mà OC ⊥ AD

⇒ OC là đường trung tuyến của ΔAOD

⇒ C là trung điểm của AD

⇒ AC = CD