Các câu hỏi tương tự
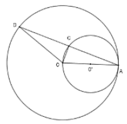
Cho đường tròn tâm O bán kính OA và đường tròn đường kính OA.
Dây AD của đường tròn lớn cắt đường tròn nhỏ ở C. Chứng minh rằng AC = CD.
Cho đường tròn tâm O bán kính OA và đường tròn đường kính OA.
a) Hãy xác định vị trí tương đối của hai đường tròn.
b) Dây AD của đường tròn lớn cắt đường tròn nhỏ ở C. Chứng minh rằng AC = CD.
Cho đường tròn (O) bán kính OA và đường tròn (O') đường kính OA. Dây AD của đường tròn lớn cắt đường tròn nhỏ tại C. Khi đó
A. AC>CD
B. AC =CD
C. AC < CD
D. CD=OD
Cho đường tròn tâm O , bán kính R và điểm A nằm ngoài đường tròn sao cho OA > 2R . Từ A kẻ hai tiếp tuyến AB , AC đến đường tròn (O) (B,C là 2 tiếp điểm ) . Trên cung nhỏ BC lấy điểm D sao cho CD < BD , tia AD cắt đường tròn (O) tại điểm E (E khác D). Qua B vẽ đường thẳng song song với AE cắt (O) tại K , CK cắt DE tại M.Vẽ tia AC cắt BE tại F .c/m nếu E là trung điểm của BF thì BC=DE
Cho đường tròn (O; R) và một điểm A trên (O). Trên đoạn OA lấy điểm B sao cho OB
1
3
OAa, Chứng minh đường tròn đường kính AB tiếp xúc với (O)b, Đường tròn (O; R) với R R cắt đường tròn đường kính AB tại C. Tia AC cắt hai đường tròn đổng tâm tại D và E với D nằm giữa C và E. Chứng minh AC CD DE
Đọc tiếp
Cho đường tròn (O; R) và một điểm A trên (O). Trên đoạn OA lấy điểm B sao cho OB = 1 3 OA
a, Chứng minh đường tròn đường kính AB tiếp xúc với (O)
b, Đường tròn (O; R') với R R' cắt đường tròn đường kính AB tại C. Tia AC cắt hai đường tròn đổng tâm tại D và E với D nằm giữa C và E. Chứng minh AC = CD = DE
Cho đường tròn tâm O bán kính R,điểm A Oke bên ngoài đường tròn,từ A vẽ 2 tiếp tuyến AB và AC với đường tròn tâm O
a)Chứng minh OA vg góc BC
b)Vẽ đường kính CD,cm BD//OA
c)AD cắt đường tròn tâm O tại E.Chứng minh AB2=AE.AD
d)Gọi I là trung điểm của ED.Cm 5 điểm O,I,B,A,C thẳng hàng
Bài 1: Từ điểm A ở bên ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến đường tròn (O) (B,C là hai tiếp điểm). Kẻ cát tuyến ADE vs đường tròn (O) (D nằm giữa A và E).a) cm: A,B,O,C cùng thuộc một đường tròn.b) cm: OA vuông BC tại H và OD2 OH.OA. Từ đó suy ra tam giác OHD đồng dạng vs tam giác ODA.c) cm: BC trùng với tia phân giác của góc DHE.d) Từ D kẻ đường thẳng song song với BE, đường thẳng này cắt AB, AC lần lượt tại M và N. cm: D là trung điểm MN.Bài 2: Cho đường tròn tâm O bán kính R,...
Đọc tiếp
Bài 1: Từ điểm A ở bên ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến đường tròn (O) (B,C là hai tiếp điểm). Kẻ cát tuyến ADE vs đường tròn (O) (D nằm giữa A và E).
a) cm: A,B,O,C cùng thuộc một đường tròn.
b) cm: OA vuông BC tại H và OD2 = OH.OA. Từ đó suy ra tam giác OHD đồng dạng vs tam giác ODA.
c) cm: BC trùng với tia phân giác của góc DHE.
d) Từ D kẻ đường thẳng song song với BE, đường thẳng này cắt AB, AC lần lượt tại M và N. cm: D là trung điểm MN.
Bài 2: Cho đường tròn tâm O bán kính R, dây BC khác đường kính. Hai tiếp tuyến của đường tròn (O,R) tại B và tại C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc vs CD tại H.
a) cm: A,B,O,C cùng thuoojcj một đường tròn. Xác định tâm và bán kính của đường tròn đó.
b) cm: AO vuông góc vs BC. Cho biết R=15cm, BC=24cm. Tính AB, OA.
c) cm: BC là tia phân giác của góc ABH.
d) Gọi I là giao điểm của AD và BH, E là giao điểm của BD và AC. cm: IH=IB.
Cho nửa đường tròn (O; R) đường kính AB. Vẽ dây CD R (C thuộc cung AD). Nối AC và BD cắt nhau tại Ma, Chứng minh rằng khi CD thay đổi vị trí trên nửa đường tròn thì độ lớn góc
A
M
B
^
không đổib, Cho
A
B
C
^
30...
Đọc tiếp
Cho nửa đường tròn (O; R) đường kính AB. Vẽ dây CD = R (C thuộc cung AD). Nối AC và BD cắt nhau tại M
a, Chứng minh rằng khi CD thay đổi vị trí trên nửa đường tròn thì độ lớn góc A M B ^ không đổi
b, Cho A B C ^ = 30 0 , tính độ dài cung nhỏ AC và diện tích hình viên phân giói hạn bởi dây AC và cung nhỏ AC
Đường tròn (O) , bán kính R , A nằm ngoài đường tròn, OA=2R . Vẽ tiếp tuyến AB của đường tròn
â) CM: Tam giác OAB vg tại B , tính AB theo R
b) Từ B kẻ dây cung vuông góc OA tại H . CM: AC là tiếp tuyến (O)
c) CM: tam giác ABC đều
đ) Từ H vẽ đường thẳng vuông góc AB tại D, đường tròn đường kính AC cắt CD tại E. CM: A,E,F thẳng hàng