Hàm số f(x)=mx+cosx đồng biến trên khoảng ( 0 ; π 2 ) khi và chỉ khi giá trị của m thuộc khoảng nào sau đây?
A. ( 0 ; + ∞ )
B. ( 1 ; + ∞ )
C. [ 1 ; + ∞ )
D. ( 0 ; + ∞ )
Những câu hỏi liên quan
Cho các mệnh đề sau (I) Hàm số f(x)
sin
x
x
2
+
1
là hàm số chẵn. (II) Hàm số f(x) 3sinx + 4cosx có giá trị lớn nhất là 5. (III) Hàm số f(x) tanx tuần hoàn với chu kì 2
π
. (IV) Hàm số f(x) cosx đồng biến trên khoảng (0;
π
) Trong các mệnh đề trên có bao nhiêu mệnh đề đúng? A. 4 B. 2 C. 3 D. 1
Đọc tiếp
Cho các mệnh đề sau
(I) Hàm số f(x) = sin x x 2 + 1 là hàm số chẵn.
(II) Hàm số f(x) = 3sinx + 4cosx có giá trị lớn nhất là 5.
(III) Hàm số f(x) = tanx tuần hoàn với chu kì 2 π .
(IV) Hàm số f(x) = cosx đồng biến trên khoảng (0; π )
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
A. 4
B. 2
C. 3
D. 1
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số ysinx+cosx+mx đồng biến trên khoảng
-
∞
;
+
∞
A
.
-
2
≤
m
≤
2
B
.
m
≤
-
2
C
.
-
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=sinx+cosx+mx đồng biến trên khoảng - ∞ ; + ∞
A . - 2 ≤ m ≤ 2
B . m ≤ - 2
C . - 2 < m < 2
D . m ≥ 2
Cho hàm số
y
f
(
x
)
có đạo hàm trên khoảng
a
;
b
. Xét các mệnh đề sau: I. Nếu hàm số
y
f
(
x
)
đồng biến trên khoảng
a
;
b
thì
f...
Đọc tiếp
Cho hàm số y = f ( x ) có đạo hàm trên khoảng a ; b . Xét các mệnh đề sau:
I. Nếu hàm số y = f ( x ) đồng biến trên khoảng a ; b thì f ' x > 0 , ∀ x ∈ a ; b .
II. Nếu f ' x < 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
III. Nếu hàm số y = f ( x ) liên tục trên a ; b và f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên đoạn a ; b .
Số mệnh đề đúng là:
A. 3
B. 0
C. 2
D. 1
Đáp án là C
I.Sai ví dụ hàm số y = x 3 đồng biến trên
(−¥; +¥) nhưng y' ³ 0, "x Î (−¥; +¥)
II.Đúng
III.Đúng
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm f(x)
x
(
x
-
1
)
2
(
x
2
+
m
x
+
9
)
. Có bao nhiêu số nguyên dương m để hàm số yf(3-x) đồng biến trên khoảng
(
3
;
+
∞
)
. A. 6. B. 8. C. 5. D. 7.
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f'(x)= x ( x - 1 ) 2 ( x 2 + m x + 9 ) . Có bao nhiêu số nguyên dương m để hàm số y=f(3-x) đồng biến trên khoảng ( 3 ; + ∞ ) .
A. 6.
B. 8.
C. 5.
D. 7.
1) tìm khoảng đồng biến nghịch biến \(y=\dfrac{x^2-6x+10}{x-3}\)
2) hàm số \(y=\dfrac{mx-4}{x-m}\) đồng biến trên khoảng (0,\(+\infty\))
1: TXĐ: D=R\{3}
\(y=\dfrac{x^2-6x+10}{x-3}\)
=>\(y'=\dfrac{\left(x^2-6x+10\right)'\left(x-3\right)-\left(x^2-6x+10\right)\left(x-3\right)'}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{\left(2x-6\right)\left(x-3\right)-\left(x^2-6x+10\right)}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{2x^2-12x+18-x^2+6x-10}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{x^2-6x+8}{\left(x-3\right)^2}\)
Đặt y'<=0
=>\(\dfrac{x^2-6x+8}{\left(x-3\right)^2}< =0\)
=>\(x^2-6x+8< =0\)
=>(x-2)(x-4)<=0
=>2<=x<=4
Vậy: Khoảng đồng biến là [2;3) và (3;4]
Đúng 1
Bình luận (0)
cho hàm số y=f(x)=-x^2-2x+1. Mệnh đề nào sau đây là đúng? A. Hàm số nghịch biến trên khoảng (-1;+vô cực) B. Hàm số nghịch biến trên khoảng (-vô cực;-1) C. Hàm số đồng biến trên khoảng (-1;+vô cực) D. Hàm số đồng biến trên khoảng (-vô cực;0)
B. Hàm số nghịch biến trên khoảng \(\left(-\infty;-1\right)\)
Đúng 3
Bình luận (0)
Cho hàm số y f(x) có đạo hàm
f
(
x
)
x
(
x
-
1
)
4
(
x
2
+
m
x
+
9
)
với mọi. Có bao nhiêu giá trị nguyên dương của m để hàm số g(x) f(3 - x) đồng biến trên khoảng
3...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f ' ( x ) = x ( x - 1 ) 4 ( x 2 + m x + 9 ) với mọi. Có bao nhiêu giá trị nguyên dương của m để hàm số g(x) = f(3 - x) đồng biến trên khoảng 3 ; + ∞
A. 5
B. 6
C. 7
D. Vô số
Cho hàm số yf(x) xác định trên
ℝ
và có đồ thị của hàm số f’(x) và các khẳng định sau:(1). Hàm số yf(x) đồng biến trên khoảng
1
;
+
∞
(2). Hàm số yf(x) nghịch biến trên khoảng
-
∞
;
-
2
(3). Hàm số yf(x) nghịch biến trên khoảng
-...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)
Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
Cho hàm số f(x) liên tục trên có f(0) 0 và đồ thị hàm số y f’(x) như hình vẽ bên. Hàm số đồng biến trên khoảng A.
2
;
+
∞
B.
-
∞
;
2
C. (0;2) D. (1;3)
Đọc tiếp
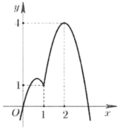
Cho hàm số f(x) liên tục trên có f(0) = 0 và đồ thị hàm số y = f’(x) như hình vẽ bên. Hàm số đồng biến trên khoảng
A. 2 ; + ∞
B. - ∞ ; 2
C. (0;2)
D. (1;3)
