Tìm tập hợp nghiệm của phương trình x lg 4 + 4 lgx = 32
A. {100} B. {10}
C. {100;10} D. {4}
Tìm tập hợp nghiệm của phương trình sau lg(152 + x 3 ) = lg ( x + 2 ) 3
A. {4} B. {-6}
C. {4;-6} D. {4;6}
Tìm tập hợp nghiệm của phương trình sau lg(152 + x 3 ) = lg x + 2 3
A. {4} B. {-6}
C. {4;-6} D. {4;6}
Tìm tập hợp nghiệm của phương trình
0 , 125 . 4 2 x = 2 8 - x
A. {6} B. {4}
C. {2} D. {1}
Tìm tập hợp nghiệm của phương trình 2 x 2 - x - 4 = 0
A. {1;2} B. {2;3}
C. {-2;3} D. {2;-3}
Tìm tập hợp nghiệm của phương trình 2 x 2 - x - 4 = 0
A. {1;2} B. {2;3}
C. {-2;3} D. {2;-3}
Cho phương trình \(4^x-2^{x+2}+m=0\). Tìm tập hợp tất cả giá trị của tham số \(m\) để phương trình đã cho có hai nghiệm phân biệt
Đặt \(t=2^x>0\).
Phương trình ban đầu trở thành: \(t^2-4t+m=0\) (*)
Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt dương:
\(\left\{{}\begin{matrix}\Delta'>0\\t_1+t_2>0\\t_1t_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4-m>0\\4>0\left(đúng\right)\\m>0\end{matrix}\right.\Leftrightarrow0< m< 4\)
Tìm tập hợp tất cả các giá trị của tham số m sao cho bất phương trình sau có nghiệm: x + 5 + 4 - x ≥ m
A. - ∞ ; 3
B. - ∞ ; 3
C. ( 3 2 ; + ∞ )
D. ( - ∞ ; 3 2 )
Tìm tập hợp tất cả các giá trị của tham số m sao cho bất phương trình sau có nghiệm: x + 5 + 4 − x ≥ m
A. − ∞ ; 3
B. − ∞ ; 3 2
C. 3 2 ; + ∞
D. − ∞ ; 3 2
Đáp án B
Điều kiện x + 5 ≥ 0 4 − x ≥ 0 ⇔ − 5 ≤ x ≤ 4
Xét hàm số f x = x + 5 + 4 − x ; x ∈ − 5 ; 4
Ta có:
f ' x = 1 2 x + 5 − 1 2 4 − x ; f ' x = 0 ⇔ 4 − x = x + 5 ⇔ x = − 1 2
Tính các giá trị f − 5 = 3 ; f 4 = 3 ; f − 1 2 = 3 2
⇒ max − 5 ; 4 f x = f − 1 2 = 3 2
Vậy để phương trình m ≤ f x có nghiệm m ≤ max − 5 ; 4 f x ⇔ m ≤ 3 2
Tìm tập hợp nghiệm của bất phương trình:
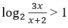
A. (- ∞ ; -2) B. (4; ∞ )
C. (- ∞ ; -2) ∪ (4; + ∞ ) D. (-2;4)
cho tập hợp A={xϵ R |\(\dfrac{2x}{x^2+1}\)≥1} ; B là tập hợp tất cả các giá trị nguyên của b để phương trình x2 -2bx+4=0 vô nghiệm .Tìm số phần tử chung của hai tập hợp trên
\(\dfrac{2x}{x^2+1}\ge1\Leftrightarrow2x\ge x^2+1\Leftrightarrow x^2-2x+1\le0\\ \Leftrightarrow\left(x-1\right)^2\le0\)
Mà \(\left(x-1\right)^2\ge0\Leftrightarrow x-1=0\Leftrightarrow x=1\)
\(A=\left\{1\right\}\)
Để \(x^2-2bx+4=0\Leftrightarrow\Delta=4b^2-4\cdot4< 0\)
\(\Leftrightarrow b^2-4< 0\Leftrightarrow\left(b-2\right)\left(b+2\right)< 0\\ \Leftrightarrow x\le-2;x\ge2\)
\(\Leftrightarrow B=\left\{x\in R|x\le-2;x\ge2\right\}\)
Vậy \(A\cap B=\varnothing\)