Có bao nhiêu giá trị nguyên của m để phương trình cos2x-4cosx-m= 0 có nghiệm
A. 6
B. 7
C. 9
D. 8
Có bao nhiêu giá trị nguyên của m để phương trình cos 2 x − 4 cos x − m = 0 có nghiệm.
A. 6
B. 7
C. 8
D. 9
Đáp án D
Ta có: P T ⇔ 2 cos 2 x − 1 − 4 cos x = m
→ t − cos x f t = 2 t 2 − 4 t − 1 = m t ∈ − 1 ; 1
Khi đó: f ' t = 4 t − 4 = 0 ⇔ t = 1
Lại có: f 1 = 5 ; f 1 = − 3 do đó PT đã cho có nghiệm
⇔ m ∈ − 3 ; 5 ⇒ có 9 giá trị nguyên của m
Có bao nhiêu giá trị nguyên của m để phương trình cos 2 x − 4 cos x − m = 0 có nghiệm
A. 6
B. 7
C. 9
D. 8
Đáp án C
Ta có
cos 2 x − 4 cos x − m = 0 ⇔ 2 cos 2 x − 1 − 4 cos x − m = 0 ⇔ 2 cos 2 x − 4 cos x − 1 = m *
Đặt t = cos x ∈ − 1 ; 1 , khi đó * ⇔ m = f t = 2 t 2 − 4 t − 1 I .
Suy ra f t là hàm số nghịch biến trên − 1 ; 1 nên để I có nghiệm − 3 ≤ m ≤ 5
Vậy có tất cả 9 giá trị nguyên của tham số m cần tìm
Có bao nhiêu số nguyên m để phương trình c o s 2 x - c o s x = m + 3 m + 4 cos x có nghiệm
A. 7.
B. 4.
C. 6.
D. 3
Cho phương trình : cos2x+4cosx+m=0 . Tìm tẩ cả các giá trị tham số m để phương trình đã cho có nghiệm
\(\Leftrightarrow2cos^2x+4cosx-1=-m\)
Xét \(f\left(x\right)=2cos^2x+4cosx-1\)
\(f\left(x\right)=2cos^2x+4cosx+2-3=2\left(cosx+1\right)^2-3\ge-3\)
\(f\left(x\right)=2cos^2x+4cosx-6+5=2\left(cosx-1\right)\left(cosx+3\right)+5\le5\)
\(\Rightarrow-3\le-m\le5\Rightarrow-5\le m\le3\)
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình cos2x + m|sinx| - m = 0 có nghiệm?
A. 0
B. 1
C. 2
D. vô số
Đáp án B
PT ![]()
![]()
Đặt ![]()
![]()
Để (1) có nghiệm thì (2) có nghiệm ![]() có nghiệm
có nghiệm ![]()
Suy ra 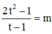 có nghiệm
có nghiệm ![]()
Xét hàm số 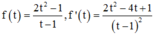
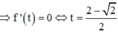
Lập bảng biến thiên hàm số 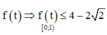
![]()
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình cos 2 x + m sinx − m = 0 có nghiệm?
A. 2
B. Vô số
C. 0
D. 1
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình cos 2 x + m sin x - m = 0 có nghiệm?
A. 0
B. 1
C. 2
D. vô số
Đáp án B
PT

Đặt
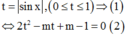
Để (1) có nghiệm thì (2) có nghiệm ![]() có nghiệm
có nghiệm ![]()
Suy ra 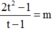 có nghiệm
có nghiệm ![]()
Xét hàm số 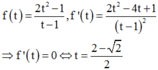
Lập bảng biến thiên hàm số 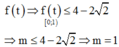
Cho phương trình m . sin x + 4 cos x = 2 m − 5 với m là tham số. Có bao nhiêu giá trị nguyên của m để phương trình có nghiệm?
A. 4.
B. 7.
C. 6.
D. 5.
Đáp án C.
Áp dụng bất đẳng thức Bunhiacopxki, ta có:
m . s inx+4cosx 2 ≤ m 2 + 4 2 sin 2 x + c os 2 x = m 2 + 16.
Nên để phương trình đã cho có nghiệm ⇔ 3 m − 5 2 ≤ m 2 + 16 ⇔ 3 m 2 20 m + 9 ≤ 0.
Kết hợp với m ∈ ℤ , ta được m = 1 ; 2 ; 3 ; 4 ; 5 ; 6 là giá trị cần tìm.
Có bao nhiêu giá trị nguyên của tham số m để phương trình cos 2 x - 3 sin 2 x - 2 3 sin x + cos x + m = 0 có nghiệm x ∈ - π 3 ; 2 π 3
A. 4
B. 3
C. 9
D. 10
Chọn đáp án C
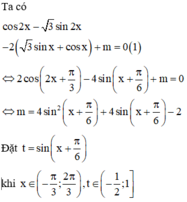

Bảng biến thiên:
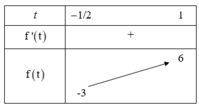
Từ bảng biến thiên ta có phương trình (1) đã cho có nghiệm

Vậy có 9 giá trị nguyên của m thỏa mãn yêu cầu bài toán.