Đáp án D
Ta có: P T ⇔ 2 cos 2 x − 1 − 4 cos x = m
→ t − cos x f t = 2 t 2 − 4 t − 1 = m t ∈ − 1 ; 1
Khi đó: f ' t = 4 t − 4 = 0 ⇔ t = 1
Lại có: f 1 = 5 ; f 1 = − 3 do đó PT đã cho có nghiệm
⇔ m ∈ − 3 ; 5 ⇒ có 9 giá trị nguyên của m
Đáp án D
Ta có: P T ⇔ 2 cos 2 x − 1 − 4 cos x = m
→ t − cos x f t = 2 t 2 − 4 t − 1 = m t ∈ − 1 ; 1
Khi đó: f ' t = 4 t − 4 = 0 ⇔ t = 1
Lại có: f 1 = 5 ; f 1 = − 3 do đó PT đã cho có nghiệm
⇔ m ∈ − 3 ; 5 ⇒ có 9 giá trị nguyên của m
Có bao nhiêu giá trị nguyên của tham số m để phương trình
m + 3 . m + cos x 3 3 = cos x có nghiệm thực?
A. 2.
B. 7.
C. 5.
D. 3.
Có bao nhiêu giá trị nguyên của tham số m để phương trình cos 3 x - cos 2 x + m cos x = 1 có đúng 7 nghiệm khác nhau thuộc khoảng - π 2 ; 2 π
A. 2
B. 4
C. Không tồn tại
D. 1
Số giá trị nguyên m để phương trình 4 m - 4 . sin x . cos x + m - 2 . cos 2 x = 3 m - 9 . Có nghiệm là:
A. 7
B. 6
C. 5
D. 4
Tổng tất cả các giá trị nguyên của m để phương trình 4 sin x + ( m - 4 ) cos x - 2 m + 5 = 0 có nghiệm là:
A. 5
B. 6
C. 10
D. 3
Có bao nhiêu giá trị nguyên của tham số m để phương trình 6 + x - 2 - x - 3 + x - 6 - x - 5 - m = 0 có nghiệm thực
A. 0
B. 2
C. 3
D. 1
Tất cả các giá trị thực của tham số m để phương trình cos 2 x - 2 m - 1 cos x - m + 1 = 0 có đúng 2 nghiệm thuộc đoạn - π 2 ; π 2 là
A. - 1 ≤ m ≤ 0
B. 0 ≤ m ≤ 1
C. - 1 ≤ m ≤ 1
D. 0 ≤ m ≤ 1
Cho phương trình m - 1 x 2 + 3 3 + x + 4 11 x 2 - 8 x + 8 = 0 . Có tất cả bao nhiêu giá trị nguyên của m để phương trình có bốn nghiệm thực phân biệt?
A. 4
B. 5
C. 6
D. 7
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d có đồ thị hàm số như hình bên dưới đây:
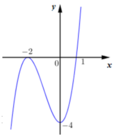
Có bao nhiêu giá trị nguyên của tham số m để phương trình f 2 ( x ) - ( m + 5 ) f ( x ) + 4 m + 4 = 0 có 7 nghiệm phân biệt?
A. 1
B. 2
C. 3
D. 4
Có tất cả bao nhiêu giá trị nguyên của m để phương trình x + 9 − x = − x 2 + 9 x + m có nghiệm?
A. 12
B. 13
C. 14
D. Vô số
Cho phương trình 3 x = a . 3 x cos ( π x ) - 9 . Có bao nhiêu giá trị thực của tham số a thuộc đoạn [ -2018; 2018] để phương trình đã cho có đúng một nghiệm thực?
A. 1
B. 2018
C. 0
D. 2