Giải phương trình sin ( 2 x + π 3 ) = - 1 2
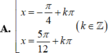



Giải các phương trình sau. π 1. 2sin( x − ) − 2 = 0 . 4 2. sin 2 x − 2 3 sin 2 x − cos x + 3 sin x = 0 .
giúp em với adim
lớp 11
Số nghiệm của phương trình sin x . sin 2 x + 2 . sin x . cos 2 x + sin x + cos x sin x + cos x = 3 . cos 2 x trong khoảng - π , π là:
A. 2
B. 4
C. 3
D. 5
Giải giúp mình phương trình này với ạ
\(sin(x-{π\over6})^3+3sin(x+{π\over3})^3=cosx+sin2x\)
phương trình nào vậy bn?
????????????????????????????????????????????????/
PT gì vậy bn
Trong các khoảng sau, m thuộc khoảng nào để phương trình sin^2 x-(2m+1) sin x.cos x + 2m cos^2 x = 0 có nghiệm thuộc khoảng (π/4 ; π/3)?
\(sin^2x-2m.sinx.cosx-sinx.cosx+2mcos^2x=0\)
\(\Leftrightarrow sinx\left(sinx-cosx\right)-2mcosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-2m.cosx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=cosx\\sinx=2m.cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=2m\end{matrix}\right.\)
Do \(tanx=1\) ko có nghiệm đã cho nên \(tanx=2m\) phải có nghiệm trên khoảng đã cho
\(\Rightarrow tan\left(\dfrac{\pi}{4}\right)< 2m< tan\left(\dfrac{\pi}{3}\right)\)
\(\Rightarrow1< 2m< \sqrt[]{3}\)
\(\Rightarrow m\in\left(\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\) (hoặc có thể 1 đáp án là tập con của tập này cũng được)
Tìm m để phương trình sin 5x=m.sin x có đúng 2 nghiệm phân biệt x thuộc [π/6;π/3]
- Giải phương trình : cos ( x - \(_{^{ }15}o\)) = \(\frac{\sqrt{2}}{2}\)
- Giải các phương trình sau và tìm các nghiệm trong đoạn [ 0;π ]
1. sin ( 3x+1)=sin(x-2)
2. sin ( x - \(^{120^o}\) )+ cos2x=0
3. sin3x + sin ( \(\frac{\pi}{4}\) - \(\frac{x}{2}\) ) = 0
Giải các phương trình sau: sin( π 2 + 2x) + 3 sin(π - 2x) = 2
A. x = ± π 6 + k2π
B. x = ± 5 π 6 + k2π
C. x = π 4 + k2π
D. x = π 6 + kπ
Tìm nghiệm x ∈ (0; π) của phương trình: 5cosx + sinx - 3 = 2 sin(2x + π 4 )
A. ![]()
B. ![]()
C. ![]()
D. Vô nghiệm
Tìm số nghiệm x ∈ (0; π) của phương trình 5cosx + sinx - 3 = 2 sin(2x + π 4 ) (*)
A: 1
B: 2
C: 3
D: 4
\(\Leftrightarrow1-2sin^2x+\left(2m-3\right)sinx+m-2=0\)
\(\Leftrightarrow2sin^2x-\left(2m-3\right)sinx-m+1=0\)
\(\Leftrightarrow2sin^2x+sinx-2\left(m-1\right)sinx-\left(m-1\right)=0\)
\(\Leftrightarrow sinx\left(2sinx+1\right)-\left(m-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2sinx+1\right)\left(sinx-m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-\dfrac{1}{2}\\sinx=m-1\end{matrix}\right.\)
Pt có đúng 2 nghiệm thuộc khoảng đã cho khi và chỉ khi:
\(\left\{{}\begin{matrix}m-1\ne-\dfrac{1}{2}\\-1\le m-1\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\0\le m\le2\end{matrix}\right.\)