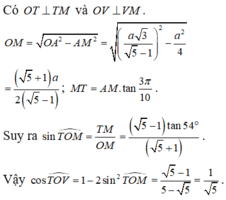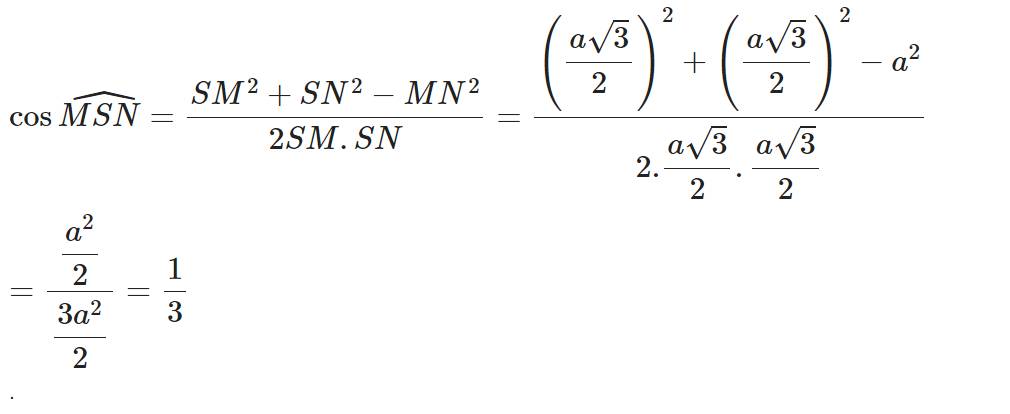Tính sin của góc tạo bởi hai mặt kề nhau (tức là hai mặt có một cạnh chung) của một tứ diện đều.

Những câu hỏi liên quan
Tính sin của góc tạo bởi hai mặt kề (tức là hai mặt có một cạnh chung) của một tứ diện đều ?
Cho tứ diện đều ABCD cạnh bằng a. Gọi M và N theo thứ tự là trung điểm của AB và CD. Khi đó góc giữa hai mặt (CAB) và (DAB) bằng \(\widehat{CMD}=2\widehat{CMN}\)
Ta có :
\(CM=\dfrac{a\sqrt{3}}{2};CN=\dfrac{a}{2}\)
Do đó :
\(\sin\widehat{CMN}=\dfrac{\dfrac{a}{2}}{\dfrac{a\sqrt{3}}{2}}=\dfrac{1}{\sqrt{3}}\)
Từ đó suy ra :
\(\sin\widehat{CMD}=\dfrac{2\sqrt{2}}{3}\)
Đúng 0
Bình luận (0)
Cho hình tứ diện đều ABCD có cạnh bằng a. Côsin của góc tạo bởi hai mặt có chung một cạnh của tứ diện đều bằng A.
2
3
B.
1
3
C.
2
4
D.
2
8
Đọc tiếp
Cho hình tứ diện đều ABCD có cạnh bằng a. Côsin của góc tạo bởi hai mặt có chung một cạnh của tứ diện đều bằng
A. 2 3
B. 1 3
C. 2 4
D. 2 8
Đáp án B
Gọi O,M lần lượt là trọng tâm tam giác BCD, trung điểm cạnh CD. Khi đó
![]()
Do đó
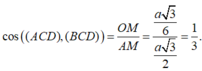
Đúng 0
Bình luận (0)
Cho hình tứ diện đều ABCD có cạnh bằng a. Côsin của góc tạo bởi hai mặt có chung một cạnh của tứ diện đều bằng A.
2
3
B.
1
3
C.
2
4
D.
2
8
Đọc tiếp
Cho hình tứ diện đều ABCD có cạnh bằng a. Côsin của góc tạo bởi hai mặt có chung một cạnh của tứ diện đều bằng
A. 2 3
B. 1 3
C. 2 4
D. 2 8
Cho hình tứ diện đều ABCD có cạnh bằng a. Côsin của góc tạo bởi hai mặt có chung một cạnh của tứ diện đều bằng A.
2
3
B.
1
3
C.
2
4
D.
2
8
Đọc tiếp
Cho hình tứ diện đều ABCD có cạnh bằng a. Côsin của góc tạo bởi hai mặt có chung một cạnh của tứ diện đều bằng
A. 2 3
B. 1 3
C. 2 4
D. 2 8
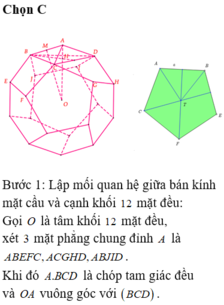
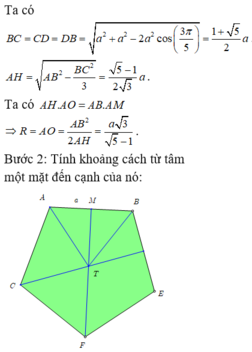
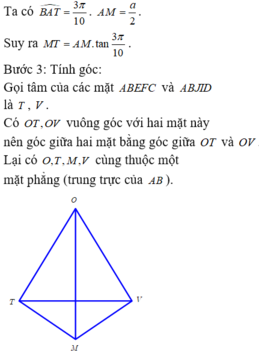
Cho hình thập nhị diện đều (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng có chung một cạnh của thập nhị diện đều bằng A.
5
-
1
2
B.
5
-
1
4
C.
1...
Đọc tiếp
Cho hình thập nhị diện đều (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng có chung một cạnh của thập nhị diện đều bằng
A. 5 - 1 2
B. 5 - 1 4
C. 1 5
D. 1 2
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính cosin của góc giữa hai mặt bên liền kề nhau.
Chứng minh:
a, Diện tích của một tam giác bằng nửa tích của hai cạnh nhân với sin của góc nhọn tạo bởi các đường thẳng chứa hai cạnh ấy
b, Diện tích của tứ giác bất kỳ bằng nửa tích của hai đường chéo nhân với sin của góc nhọn tạo bởi hai đường chéo
a, Giả sử tam giác ABC có A ^ < 90 0 kẻ đường cáo BH. Ta có BH=AB.sin A ^
=> S ∆ A B C = 1 2 A C . B H = 1 2 A B . A C . sin A
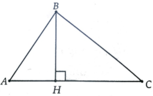
b, Giả sử tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O có
A
O
B
^
=
α
<
90
0
. Kẻ AH
⊥
BD, tại H và CK
⊥
BD tại K
Ta có: AH = OA.sinα
=> S A B D = 1 2 B D . A H = 1 2 B D . O A . sin α
Tương tự: S C B D = 1 2 B D . C K = 1 2 B D . O C . sin α
=> S A B C D = S A B D + S C B D = 1 2 B D . O A . sin α + 1 2 B D . O C . sin α = 1 2 B D . A C . sin α

Đúng 1
Bình luận (0)
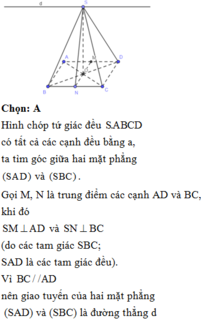
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính cosin của góc giữa hai mặt bên không liền kề nhau.
A. 1 3
B. 1 2
C. 1 2
D. 5 3
Phương pháp:
+ Sử dụng định nghĩa để tìm góc giữa hai mặt phẳng (P) và (Q):
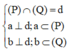
khi đó góc giữa (P) và (Q) chính là góc giữa hai đường thẳng a và b.
+ Sử dụng định lý hàm số cos trong tam giác để tính toán:
Cho tam giác ABC khi đó ![]()
Cách giải:

Hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a, ta tìm góc giữa hai mặt phẳng (SAD) và (SBC).
Gọi M, N là trung điểm các cạnh AD và BC, khi đó SM ⊥ AD và SN ⊥ BC (do các tam giác SBC;SAD là các tam giác đều).
Vì BC//AD nên giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng d qua S và song song AD, BC.
Vì SM
⊥
AD và SN
⊥
BC nên SM
⊥
d và SN
⊥
d mà ![]() góc giữa hai mặt phẳng (SAD) và (SBC) là góc MSN.
góc giữa hai mặt phẳng (SAD) và (SBC) là góc MSN.
Mặt bên là các tam giác đều cạnh a nên ![]()
Khi đó: ![]()
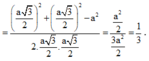
Chọn A
Chú ý khi giải:
Các em có thể tính SO theo tỉ số lượng giác và suy ra MSN = 2MSO
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính cosin của góc giữa hai mặt bên không liền kề nhau
A. 1 3
B. 1 2
C. 1 2
D. 5 3