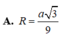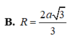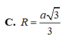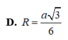Cho tứ diện đều ABCD cạnh bằng a. Gọi M và N theo thứ tự là trung điểm của AB và CD. Khi đó góc giữa hai mặt (CAB) và (DAB) bằng ∠ CMD = 2 ∠ CMN
Ta có: ![]()
Do đó: 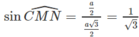
Từ đó suy ra: ![]()
Cho tứ diện đều ABCD cạnh bằng a. Gọi M và N theo thứ tự là trung điểm của AB và CD. Khi đó góc giữa hai mặt (CAB) và (DAB) bằng ∠ CMD = 2 ∠ CMN
Ta có: ![]()
Do đó: 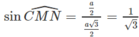
Từ đó suy ra: ![]()
Cho hình thập nhị diện đều (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng có chung một cạnh của thập nhị diện đều bằng
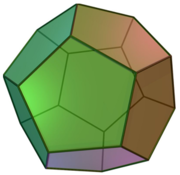
A. 5 - 1 2
B. 5 - 1 4
C. 1 5
D. 1 2
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính cosin của góc giữa hai mặt bên không liền kề nhau.
A. 1 3
B. 1 2
C. 1 2
D. 5 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều và nằm trong một mặt phẳng vuông góc với đáy. Gọi H, K lần lượt là trung điểm của các cạnh AB và AD. Tính sin của góc tạo bởi giữa đường thẳng SA và mặt phẳng (SHK)
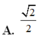
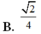
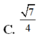
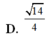
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng α . Cô sin của góc tạo bởi 2 mặt phẳng (SAD) và (SBC) bằng
![]()
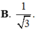
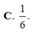

Cosin góc tạo bởi cạnh bên và mặt đáy của hình chóp tứ giác đều có tất cả các cạnh bằng nhau là
A. 1 3
B. 1 3
C. 3 2
D. 1 2
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a 3 , BD = 3a. hình chiếu vuông góc của B lên mặt phẳng (A'B'C'D') là trung điểm của A'C'. Biết rằng côsin của góc tạo bởi hai mặt phẳng (ABCD) và (CDD'C') bằng 21 7 . Tính theo a bán kính mặt cầu ngoại tiếp tứ diện A'BC'D'.
A. a
B. 2a
C. 3a
D. a 2
Khẳng định nào sau đây sai?
A. Hình lập phương là đa diện lồi.
B. Tứ diện là đa diện lồi.
C. Hình hộp là đa diện lồi.
D. Hình tạo bởi hai khối lăng trụ có chung nhau một mặt bên là một hình đa diện lồi.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh α , tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt đáy. Gọi H, K lần lượt là trung điểm của AB, AD. Tính sin của góc tạo bởi đường thẳng SA và mặt phẳng (SHK)
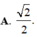
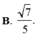
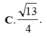
Cho lăng trụ tam giác ABC.A'B'C' có đáy là tam giác đều cạnh bằng a, góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30 ∘ . Biết hình chiếu vuông góc của A' trên (ABC) trùng với trung điểm cạnh BC. Tính theo a bán kính mặt cầu ngoại tiếp tứ diện A'.ABC