Cho vectơ a, b là hai vectơ khác vectơ 0. Khi nào có đẳng thức
Những câu hỏi liên quan
Cho hai vectơ
a
→
,
b
→
khác vectơ
0
→
, không cùng phương và có độ dài bằng nhau. Khi đó giá của hai vectơ
a
→
+
b
→
và
a
→
-
b
→
thỏa mãn điều kiện nào sau đây? A. Cắt và không vuông góc B. Vuông góc với nhau C. Song...
Đọc tiếp
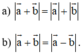
Cho hai vectơ a → , b → khác vectơ 0 → , không cùng phương và có độ dài bằng nhau. Khi đó giá của hai vectơ a → + b → và a → - b → thỏa mãn điều kiện nào sau đây?
A. Cắt và không vuông góc
B. Vuông góc với nhau
C. Song song với nhau
D. Trùng nhau
Cho hai vectơ a→ và b→đều khác 0→. Khi nào thì tích vô hướng của hai vectơ đó là số dương ? Là số âm ? Bằng 0 ?
Cho
a
→
và
b
→
là hai vectơ cùng hướng và đều khác vectơ
0
→
. Mệnh đề nào sau đây đúng? A.
a
→
.
b
→
a
→
.
b
→
B.
a
→
.
b...
Đọc tiếp
Cho a → và b → là hai vectơ cùng hướng và đều khác vectơ 0 → . Mệnh đề nào sau đây đúng?
A. a → . b → = a → . b →
B. a → . b → = 0
C. a → . b → = − 1
D. a → . b → = − a → . b →
Cho hai vectơ
a
→
và
b
→
khác
0
→
. Xác định góc α giữa hai vectơ
a
→
và
b
→
khi
a
→
.
b
→
−
a
→
.
b...
Đọc tiếp
Cho hai vectơ a → và b → khác 0 → . Xác định góc α giữa hai vectơ a → và b → khi a → . b → = − a → . b → .
A. α = 180 0 .
B. α = 0 0 .
C. α = 90 0 .
D. α = 45 0 .
Ta có a → . b → = a → . b → . c o s a → , b → .
Mà theo giả thiết a → . b → = − a → . b →
Suy ra cos a → , b → = − 1 ⇒ a → , b → = 180 0 .
Chọn A.
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB có trung điểm I . Gọi M là trung điểm đoạn IB. Khẳng định nào sau đây đúng? A. Vectơ AM - 3 vectơ BM = vectơ 0 B. Vectơ AM + 3 vectơ MB = vectơ 0 C. Vectơ MA +3 vectơ BM = vectơ 0 D. Vectơ AM + 3 vectơ BM = vectơ 0 ( Giải chi tiết giúp mình ạ )
ta có: I là trung điểm của AB
=>\(IA=IB=\dfrac{AB}{2}\)
M là trung điểm của IB
=>\(MI=MB=\dfrac{IB}{2}=\dfrac{AB}{4}\)
AM=AI+IM=1/2AB+1/4AB=3/4AB
=>AM=MB
=>\(\overrightarrow{AM}=3\overrightarrow{MB}\)
=>\(\overrightarrow{AM}-3\overrightarrow{MB}=\overrightarrow{0}\)
=>\(\overrightarrow{AM}+3\overrightarrow{BM}=\overrightarrow{0}\)
=>Chọn C
Đúng 1
Bình luận (0)
Trong không gian cho ba vectơ a , b và c đều khác vectơ 0 . Khi nào ba véc tơ đó đồng phẳng?
Ba vectơ a → ; b → v à c → đồng phẳng nếu thỏa mãn một trong hai điều kiện sau:
- Giá của 3 vector đều cùng song song với mặt phẳng (P).
- 1 trong 3 vec tơ biểu diễn được qua hai vec tơ còn lại,
tức là tồn tại cặp số (m; n) duy nhất thỏa mãn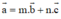 
Đúng 0
Bình luận (0)
Cho hình vuông ABCD tâm O có độ dài cạnh =6. Gọi E là điểm trên đường thẳng AC thỏa vectơ AC=3 vectơ AE và M là trung điểm AD. Chứng minh đẳng thức vectơ EB+vectơ EC+vectơ ED= vectơ AC
Cho tứ diện ABCD. Hỏi có bao nhiêu vectơ khác vectơ 0 → mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD
A. 12
B. 4
C. 10
D. 8
Đáp án A.
Với mỗi cách chọn ra 2 đỉnh bất kỳ của tứ diện ta được 2 vecto đối nhau.
Do đó có 2 C 4 2 = 12 vecto.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Hỏi có bao nhiêu vectơ khác vectơ 0 → mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD ?
A. 12
B. 4
C. 10
D. 8
Chọn A
Số vectơ khác vectơ 0 → mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD là số các chỉnh hợp chập 2 của phần tử => số vectơ là A 4 2 = 12
Đúng 0
Bình luận (0)