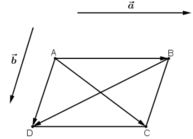
Có hai vec tơ a→, b→ bất kì như hình vẽ.
Vẽ hình bình hành ABCD sao cho 
Ta có:
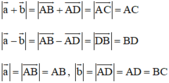
Do đó
a) 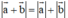 ⇔ AC = AB + BC ⇔ B nằm giữa A và C
⇔ AC = AB + BC ⇔ B nằm giữa A và C
⇔ 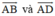 cùng hướng hay a→ và b→ cùng hướng.
cùng hướng hay a→ và b→ cùng hướng.
b) 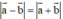 ⇔ AC = BD
⇔ AC = BD
⇔ ABCD là hình chữ nhật
⇔ AB ⊥ CD hay 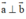

Có hai vec tơ a→, b→ bất kì như hình vẽ.
Vẽ hình bình hành ABCD sao cho 
Ta có:
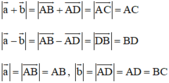
Do đó
a) 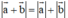 ⇔ AC = AB + BC ⇔ B nằm giữa A và C
⇔ AC = AB + BC ⇔ B nằm giữa A và C
⇔ 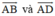 cùng hướng hay a→ và b→ cùng hướng.
cùng hướng hay a→ và b→ cùng hướng.
b) 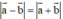 ⇔ AC = BD
⇔ AC = BD
⇔ ABCD là hình chữ nhật
⇔ AB ⊥ CD hay 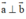
Cho hai vectơ a → , b → khác vectơ 0 → , không cùng phương và có độ dài bằng nhau. Khi đó giá của hai vectơ a → + b → và a → - b → thỏa mãn điều kiện nào sau đây?
A. Cắt và không vuông góc
B. Vuông góc với nhau
C. Song song với nhau
D. Trùng nhau
Cho hai vectơ a→ và b→đều khác 0→. Khi nào thì tích vô hướng của hai vectơ đó là số dương ? Là số âm ? Bằng 0 ?
Cho a → và b → là hai vectơ cùng hướng và đều khác vectơ 0 → . Mệnh đề nào sau đây đúng?
A. a → . b → = a → . b →
B. a → . b → = 0
C. a → . b → = − 1
D. a → . b → = − a → . b →
Cho hai vectơ a → và b → khác 0 → . Xác định góc α giữa hai vectơ a → và b → khi a → . b → = − a → . b → .
A. α = 180 0 .
B. α = 0 0 .
C. α = 90 0 .
D. α = 45 0 .
Cho đoạn thẳng AB có trung điểm I . Gọi M là trung điểm đoạn IB. Khẳng định nào sau đây đúng? A. Vectơ AM - 3 vectơ BM = vectơ 0 B. Vectơ AM + 3 vectơ MB = vectơ 0 C. Vectơ MA +3 vectơ BM = vectơ 0 D. Vectơ AM + 3 vectơ BM = vectơ 0 ( Giải chi tiết giúp mình ạ )
Cho hình vuông ABCD tâm O có độ dài cạnh =6. Gọi E là điểm trên đường thẳng AC thỏa vectơ AC=3 vectơ AE và M là trung điểm AD. Chứng minh đẳng thức vectơ EB+vectơ EC+vectơ ED= vectơ AC
Cho a → và b → là hai vectơ cùng hướng và đều khác vectơ 0 → . Trong các kết quả sau đây, hãy chọn kết quả đúng:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hai vectơ a và b đều khác vectơ 0. Các khẳng định sau đúng hay sai?
a, Hai vecto cùng hướng thì cùng phương.
b, Hai vecto b→ và kb→ cùng phương.
c, Hai vecto a→ và (-2)a→ cùng hướng.
d) Hai vector ngược hướng với vector thứ ba khác vectơ 0→ thì cùng phương.
Cho vectơ a = (2; -2), vectơ b = (1; 4). Hãy phân tích vectơ c (5; 0) theo hai vectơ a và b.