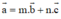
Ba vectơ a → ; b → v à c → đồng phẳng nếu thỏa mãn một trong hai điều kiện sau:
- Giá của 3 vector đều cùng song song với mặt phẳng (P).
- 1 trong 3 vec tơ biểu diễn được qua hai vec tơ còn lại,
tức là tồn tại cặp số (m; n) duy nhất thỏa mãn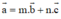 
Trong mặt phẳng Oxy, cho điểm A(2;1) và véc tơ a → (1;3). Phép tịnh tiến theo vectơ a → biến điểm A thành điểm A'. Tọa độ điểm A' là
A. (-1;-2)
B. (1;2)
C. (4;3)
D. (3;4)
Cho ba vecto a → , b → , c → trong không gian. Chứng minh rằng nếu m a → + n b → + p c → = 0 → và một trong ba số m, n, p khác không thì ba vecto a → , b → , c → đồng phẳng
Trong không gian cho hai hình bình hành ABCD và A’B’C’D’ chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ B B ' → , C C ' → , D D ' → đồng phẳng.
Trên mặt phẳng cho 6 điểm phân biệt A, B, C, D, E; F. Hỏi có bao nhiêu vectơ khác vectơ – không, mà có điểm đầu và điểm cuối là các điểm đã cho ?
A. 100.
B. 120.
C. 30.
D. 25.
Trên mặt phẳng, cho bốn điểm phân biệt A, B, C, D. Liệt kê tất cả các vectơ khác vectơ – không mà điểm đầu và điểm cuối của chúng thuộc tập điểm đã cho.
Trong mặt phẳng cho một tập hợp gồm 6 điểm phân biệt. Có bao nhiêu vectơ khác vectơ 0 → có điểm đầu và điểm cuối thuộc tập hợp điểm này?
A. 15
B. 12
C. 1440
D. 30
Cho hai vecto a → và b → đều khác vecto 0 . Hãy xác định vecto c → = 2 a → - b → và giải thích tại sao ba vecto a → , b → , c → đồng phẳng
Cho tứ diện ABCD và các điểm M,N xác định bởi A M → = 2 A B → — 3 A C → ; D N → = D B → + x D C → Tìm x để ba véc tơ A D → , B C → , M N → đồng phẳng.
A. x=-1
B. x=-3
C. x=-2
D. x=2
Trong mặt phẳng cho 10 điểm phân biệt. Số vectơ khác 0 ⇀ , có điểm đầu và điểm cuối lấy trong các điểm đã cho là
A . 2 10
B . A 10 2
C. 10!
D . C 10 2
