Giả sử p ≠ 0 ta có:
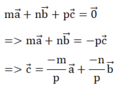
Do đó, ba vecto a → , b → , c → đồng phẳng theo định lí 1
Giả sử p ≠ 0 ta có:
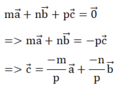
Do đó, ba vecto a → , b → , c → đồng phẳng theo định lí 1
Cho hai vecto a → và b → đều khác vecto 0 . Hãy xác định vecto c → = 2 a → - b → và giải thích tại sao ba vecto a → , b → , c → đồng phẳng
Ba vecto a → , b → , c → không đồng phẳng nếu?
A. Ba đường thẳng chứa chúng không cùng một mặt phẳng.
B. Ba đường thẳng chứa chúng cùng thuộc một mặt phẳng.
C. Ba đường thẳng chứa chúng không cùng song song với một mặt phẳng.
D. Ba đường thẳng chứa chúng cùng song song với một mặt phẳng.
Cho ba vecto n → , a → , b → bất kì đều khác với vecto 0 → . Nếu vecto n → vuông góc với cả hai vecto a → v à b → thì n → , a → v à b → :
A. đồng phẳng
B. không đồng phẳng
C. có giá vuông góc với nhau từng đôi một
D. có thể đồng phẳng
Nếu ba vecto a → , b → , c → cùng vuông góc với vecto n → khác 0 → thì chúng.
A. đồng phẳng
B. không đồng phẳng
C. có thể đồng phẳng
D. có thể không đồng phẳng
Cho ba vecto a → , b → , c → . Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng.
A. Một trong ba vecto đó bằng 0 → .
B. Có hai trong ba vecto đó cùng phương.
C. Có một vecto không cùng hướng với hai vecto còn lại
D. Có hai trong ba vecto đó cùng hướng.
Cho ba vecto a → , b → , c → . Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng?
A. Một trong ba vecto đó bằng 0 →
B. Có hai trong ba vecto đó cùng phương
C. Có một vecto không cùng hướng với hai vecto còn lại.
D. Có hai trong ba vecto đó cùng hướng
Trong không gian cho hai vecto a → và b → đều khác vecto không. Hãy xác định các vecto m → = 2 a → , n → = - 3 b → v à p → = m → + n →
Trong không gian cho ba vectơ a , b và c đều khác vectơ 0 . Khi nào ba véc tơ đó đồng phẳng?
Điều kiện cần và đủ để ba vecto a → , b → , c → không đồng phẳng là:
A. Ba đường thẳng chứa chúng không cùng thuộc một mặt phẳng.
B. Ba đường thẳng chứa chúng cùng thuộc một mặt phẳng.
C. Ba đường thẳng chứa chúng không cùng song song với một mặt phẳng.
D. Ba đường thẳng chứa chúng cùng song song với một mặt phẳng.