Các câu hỏi tương tự
Cho ba vecto
a
→
,
b
→
,
c
→
. Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng. A. Một trong ba vecto đó bằng
0
→
. B. Có hai trong ba vecto đó cùng phương. C. Có một vecto không cùng hướng với hai vecto còn lại D. Có hai trong ba vecto đó cùng hướng.
Đọc tiếp
Cho ba vecto a → , b → , c → . Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng.
A. Một trong ba vecto đó bằng 0 → .
B. Có hai trong ba vecto đó cùng phương.
C. Có một vecto không cùng hướng với hai vecto còn lại
D. Có hai trong ba vecto đó cùng hướng.
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, BC, CD, và DA.Vecto
A
C
→
cùng với hai vecto nào sau đây là ba vecto không đồng phẳng? A.
A
B
→
v
à
A
D
→
B.
M...
Đọc tiếp
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, BC, CD, và DA.
Vecto A C → cùng với hai vecto nào sau đây là ba vecto không đồng phẳng?
A. A B → v à A D →
B. M N → v à A D →
C. Q M → v à B D →
D. Q P → v à C D →
Cho ba vecto
a
→
,
b
→
,
c
→
trong không gian. Chứng minh rằng nếu
m
a
→
+
n
b
→
+
p
c
→
0...
Đọc tiếp
Cho ba vecto a → , b → , c → trong không gian. Chứng minh rằng nếu m a → + n b → + p c → = 0 → và một trong ba số m, n, p khác không thì ba vecto a → , b → , c → đồng phẳng
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, BC, CD, và DA.Vecto
M
N
→
cùng với hai vecto nào sau đây là ba vecto đồng phẳng? A.
M
A
→
v
à
M
Q
→
B.
M...
Đọc tiếp
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, BC, CD, và DA.
Vecto M N → cùng với hai vecto nào sau đây là ba vecto đồng phẳng?
A. M A → v à M Q →
B. M D → v à M Q →
C. A C → v à A D →
D. M P → v à C D →
Cho hai vecto
a
→
và
b
→
đều khác vecto
0
. Hãy xác định vecto
c
→
2
a
→
-
b
→
và giải thích tại sao ba vecto
a
→
,
b...
Đọc tiếp
Cho hai vecto a → và b → đều khác vecto 0 . Hãy xác định vecto c → = 2 a → - b → và giải thích tại sao ba vecto a → , b → , c → đồng phẳng
Cho hai vecto
a
→
và
b
→
không cùng phương. Hai vecto nào sau đây cùng phương? A. B. C. D.
Đọc tiếp
Cho hai vecto a → và b → không cùng phương. Hai vecto nào sau đây cùng phương?
A. 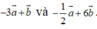
B. 
C. 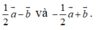
D. 
Cho hai vecto
a
→
và
b
→
không cùng phương. Hai vecto nào sau đây là cùng phương? A. B. C. D.
Đọc tiếp
Cho hai vecto a → và b → không cùng phương. Hai vecto nào sau đây là cùng phương?
A. ![]()
B. 
C. 
D. 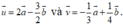
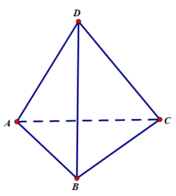
Cho hình tứ diện ABCD. Hãy chỉ ra các vecto có điểm đầu là A và điểm cuối là các điểm còn lại của hình tứ diện. Các vecto đó có cùng nằm trong một mặt phẳng không?
Cho vecto
n
→
≠
0
→
và hai vecto
a
→
v
à
b
→
không cùng phương. Nếu vecto
n
→
vuông góc với cả hai vecto
a
→
v
à
b
→
thì
n
→
,
a
→...
Đọc tiếp
Cho vecto n → ≠ 0 → và hai vecto a → v à b → không cùng phương. Nếu vecto n → vuông góc với cả hai vecto a → v à b → thì n → , a → v à b → :
A. đồng phẳng
B. không đồng phẳng
C. có thể đồng phẳng
D. có thể không đồng phẳng



