Các câu hỏi tương tự
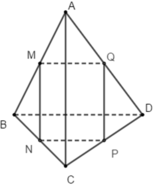
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, BC, CD, và DA.Vecto
M
N
→
cùng với hai vecto nào sau đây là ba vecto đồng phẳng? A.
M
A
→
v
à
M
Q
→
B.
M...
Đọc tiếp
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, BC, CD, và DA.
Vecto M N → cùng với hai vecto nào sau đây là ba vecto đồng phẳng?
A. M A → v à M Q →
B. M D → v à M Q →
C. A C → v à A D →
D. M P → v à C D →
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, AC, CD và DB.Bộ ba vecto không đồng phẳng là: A.
A
B
→
,
M
N
→
,
C
A
→
B.
M
P
→...
Đọc tiếp
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, AC, CD và DB.
Bộ ba vecto không đồng phẳng là:
A. A B → , M N → , C A →
B. M P → , B C → , A D →
C. A D → , M P → , P Q →
D. M P → , P Q → , P D →
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, AC, CD và DB.Bộ ba vecto đồng phẳng là: A.
A
B
→
,
B
C
→
,
A
D
→
B.
M
P
→
,
B...
Đọc tiếp
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, AC, CD và DB.
Bộ ba vecto đồng phẳng là:
A. A B → , B C → , A D →
B. M P → , B C → , A D →
C. A C → , M P → , B D →
D. M P → , P Q → , C D →
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt
A
B
→
a
→
;
A
A
→
b
→
;
...
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt A B → = a → ; A A ' → = b → ; A D → = c → .
Vecto M N → bằng:
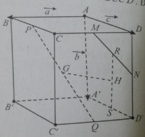
A. 1 2 c → - a →
B. 1 2 c → - b →
C. 1 2 b → - a →
D. 1 2 a → - b →
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Lấy hai điểm P và Q lần lượt thuộc AD và BC sao cho
P
A
→
m
P
D
→
và
Q
B
→
m
Q
C
→
, với m khác 1. Vecto
M
P...
Đọc tiếp
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Lấy hai điểm P và Q lần lượt thuộc AD và BC sao cho P A → = m P D → và Q B → = m Q C → , với m khác 1. Vecto M P → bằng:
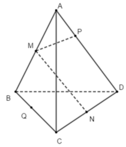
A. M B → − m Q C →
B. M N → − m P D →
C. M A → − m P D →
D. M N → − m Q C →
Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của AB và CD. Đặt
A
B
→
b
→
;
A
C
→
c
→
;
A
D
→...
Đọc tiếp
Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của AB và CD. Đặt A B → = b → ; A C → = c → ; A D → = d . Khẳng định nào sau đây đúng?
![]()
![]()
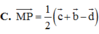
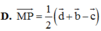
Cho bốn điểm A, B, C và D không đồng phẳng. Gọi I, K lần lượt là trung điểm của AD và BC.
a) Tìm giao tuyến của hai mặt phẳng (IBC) và (KAD).
b) Gọi M và N là hai điểm lần lượt lấy trên hai đoạn thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng (IBC) và (DMN).
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Mặt phẳng α qua MN cắt AD; BC lần lượt tại P và Q. Biết MP cắt NQ tại I. Ba điểm nào sau đây thẳng hàng?
A. I; A; C
B. I; B; D
C. I; A: B
D. I; C; D
Cho tứ diện ABCD và đặt
A
B
→
a
→
,
A
C
→
b
→
v
à
A
D
→
c
→...
Đọc tiếp
Cho tứ diện ABCD và đặt A B → = a → , A C → = b → v à A D → = c → . Gọi M là trung điểm của CD.
Vecto C D → bằng:
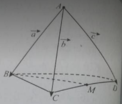
A. c → - b →
B. b → - c →
C. c → + b →
D. a → + b → + c →