Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Khi đó B C → bằng
A. 5
B. 6
C. 7
D. 9
Cho tam giác ABC vuông tại A có AB : AC = 4 : 5 và đường cao AH bằng 12cm. Khi đó độ dài đoạn thẳng HB bằng
A. 6cm; B. 9,6cm; C. 12cm; D. 15cm.
Hãy chọn phương án đúng.
*Trong các bài (1.3, 1.4, 1.5) ta sẽ sử dụng các kí hiệu sau đây đối với tam giác ABC vuông tại A có đường cao AH:
AB = c, AC = b, BC = a, AH = h, BH = c’, CH = b’.
Hướng dẫn:
∆
ABC ∼
∆
HBA nên 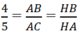
Suy ra HB = 4/5HA = 48/5 = 9,6. Chọn B.
Cho tam giác ABC vuông tại B. khi đó sin C bằng A. AB/BC B. AC/AB C. BC/AB D AB/AC
Cho tam giác ABC vuông tại A có AB : AC = 3 : 4 và đường cao AH bằng 9cm. Khi đó độ dài đoạn thẳng HC bằng
A. 6cm; B. 9cm; C. 12cm; D. 15cm.
Hãy chọn phương án đúng.
Hướng dẫn:
∆
ABC ∼
∆
HAC nên 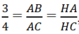
Suy ra HC = 4/3HA = 12. Chọn C.
Tam giác ABC vuông tại A cao AB = 3cm ; AC = 4 cm thì cạnh huyền BC bằng:
A. 5 cm B. 6 cm C. 7 cm D. 8 cm
Câu 1. Cho tam giác ABC cân tại A, có góc A = 70°. Số đo góc B là
A. 50° B. 60° C. 55° D. 75°
Câu 2. Cho tam giác ABC cân tại A, góc B = 75°. Số đo của góc A là
A. 40° C. 15° C. 105° D. 30°
Câu 3. Tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng:
A MN^+ NP^= MP^
B MP ^+NP^ =MN^
C NM= NP
D pN^+ MP^= MN^
Câu 4. Cho tam giác ABC vuông tại A, AB = 5 cm, AC = 12 cm. Độ dài cạnh BC là
A. 17 cm B. 13 cm C. 14 cm D. 14,4 cm
Câu 5. Cho tam giác HIK vuông tại I, IH = 10 cm, HK = 16 cm. Độ dài cạnh IK là
A. 26 cm
B. \(\sqrt{156}cm\)
C \(\sqrt{12}cm\)
D. 156cm
Câu 6. Cho tam giác ABC cân tại A, AH vuông góc với BC tại H, AB = 10cm. BC = 12 cm.
Độ dài AH bằng
A. 6cm. B. 4 cm C. 8cm D. 64 cm
Câu 7. Cho tam giác đều ABC có độ dài cạnh là 6 cm. Kẻ AI vuông góc với BC. Độ dài cạnhAI là
A. \(3\sqrt{3}cm\)
B. 3 cm
C. \(3\sqrt{2}\)
D. 4 cm
Câu 8. Một chiếc tivi có chiều rộng là 30 inch, đường chéo là 50 inch. Chiều dài chiếc tivi đó là
A. 20 inch B. 1600 inch 3400 inch. D. 40 inch
Câu 9. Tam giác vuông là tam giác có độ dài ba cạnh là:
A. 3cm, 4cm,5cm B. 5cm, 7cm, 8cm C. 4cm, 6 cm, 8cm D. 3cm, 5cm, 7cm
Câu 10. Tam giác ABCcân tại A. Biết AH = 3cm, HC = 2 cm. Khi đó độ dài BC bằng
A. 5 cm
B. 4cm
C.\(2\sqrt{5}cm\)
D \(2\sqrt{3}cm\)
Giups mik vs mik đg cần gấp
Câu 1. Trong một tam giác vuông, kết luận nào sau đây là đúng ?
A. Tổng hai góc nhọn bằng 180 0 B. Hai góc nhọn bằng nhau
C. Hai góc nhọn phô nhau D. Hai góc nhọn kề nhau .
Câu 2: Chọn câu trả lời đúng. Cho tam giác ABC có 00
A50;B60 thì C?
A. 70 0 B. 110 0 C. 90 0 D. 50 0
Câu 3. Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:
A. 1cm ; 2cm ; 3cm B. 2cm ; 3cm ; 4cm
C. 3cm ; 4cm ; 5cm D. 4cm ; 5cm ; 6cm
Câu 4: Chọn câu sai.
A. Tam giác có hai cạnh bằng nhau là tam giác cân.
B. Tam giác có ba cạnh bằng nhau là tam giác đều.
C. Tam giác cân là tam giác đều.
D. Tam giác đều là tam giác cân.
Câu 5: Tam giác ABC vuông tại B suy ra:
A. AB 2 = BC 2 + AC 2 B. BC 2 = AB 2 + AC 2
C. AC 2 = AB 2 + BC 2 D. Cả a,b,c đều đúng
Câu 6: Hãy điền dấu X vào ô trống mà em đã chọn :
Câu Nội dung Đúng Sai
1 Tam giác vuông có một góc bằng 045 là tam giác vuông cân
2 Tam giác cân có một góc bằng 060 là tam giác đều
3 Nếu ABC là một tam giác đều thì ABC là tam giác cân
4 Nếu hai cạnh và một góc của tam giác này bằng hai cạnh và
một góc của tam giác kia thì hai tam giác đó bằng nhau
Câu 7: a). Cho ABC vuông tại A có AB = 8 cm; AC = 6 cm thì BC bằng :
A. 25 cm B. 14 cm C. 100 cm D. 10 cm
b). Cho ABC cân tại A, biết 050B thì A bằng :
A. 080 B. 050 C. 0100 D. Đáp án khác
Câu 8 . Tam giác ABC có:
A. 0ABC90 B. 0ABC180 C. 0ABC45 D. 0ABC0
Câu 9: ABC = DEF Trường hợp cạnh – góc – cạnh nếu
A. AB = DE; BF ; BC = EF B. AB = EF; BF ; BC = DF
C. AB = DE; BE ; BC = EF D. AB = DF; BE ; BC = EF
Câu 10. Góc ngoài của tam giác bằng :
A. Tổng hai góc trong không kề với nó. B. Tổng hai góc trong
C. Góc kề với nó D. Tổng ba góc trong của tam giác.
Câu 1: C
Câu 2:A
Câu 3:C
Câu 4 C
Câu 5: B
Câu 6 1Đ, 2Đ, 3Đ, 4S
Câu 7: a, Đ
Câu 10 A.
Các câu khác k rõ đề
Cho
ABC có BC = 6 cm và BC = m 0 ( m 0 < 90 0 ) . Tia phân giác của góc A cắt BC tại D.
1) Tính số đo A của ABC khi m = 40 0 ;
2) Chứng minh rằng:
a) ABC cân b) ADB = ADC c) DB = DC d) AD BC
3) Tìm giá trị của m để :
a) ABC là tam giác đều b) ABC là tam giác vuông cân
4) Xác định độ dài AB để ABC là tam giác đều. Khi đó AD có độ dài bằng bao nhiêu ? Diện tích
ABC bằng bao nhiêu ?
5) Kẻ DH AC ( H
AC), DK AB (K
AB ).CMR:
a) DH = DK b) BH = CK c) HK // BC
6) Kẻ phân giác góc B và góc C cắt AD tại I. Tính số đo góc BIC theo m 0 ?
bài này dài lắm ko ai giải đâu
dai den bao gio moi xong lol
Bài 7: a, Cho tam giác ABC vuông tại A có AB 3 AC 4 = và BC = 5. Tính độ dài AB, AC b, Tính độ dài cạnh huyền biết độ dài hai cạnh góc vuông là 6 và 7 c, Tính góc ở đỉnh của tam giác cân biết số đo góc ở đáy là 200 d, Tính số đo góc ở đáy tam giác cân biết số đo góc ở đỉnh là 600
b: Độ dài cạnh huyền là \(\sqrt{6^2+7^2}=\sqrt{85}\left(cm\right)\)
c: Số đo góc ở đỉnh là:
\(180-2\cdot20^0=140^0\)
d: Số đó góc ở đáy là:
\(\dfrac{180^0-60^0}{2}=60^0\)
bài 2: tính gtri bthuwc
b) B= 3x^2+8x-1 tại x thỏa mãn (x^2+4)(x-1)=0
bài 3: Với gtri nào của biến thì mỗi bthuwc sau có GTNN, tìm gtri đó
a, A=(x-1)^2+(y-1)^2
b,B=|x-3|+y^2-10
bài 5: cho tam giác abc có góc bac = 120, đg pgiac trg góc a cắt bc tại d và từ d kẻ de vuông với ab, df vuông với ac.CM: qua c vẽ đg thg // ad cắt ab tại m và cmr tam giác acm là tam giác đều
bài 6: cho tam giác abc cân tại a lấy m bất kì trên bc kẻ mn vuông với ab mq vuông với ac bh vuông với ac mi vuông với bh. CM
a, tamgaics nbm= tam giác imb
b, mq=ih
c, mn+mq ko đổi
bài 7: cho tam giác abc co s ab=ac góc a 90 qua a kẻ đg d ko cắt cạnh bc của tam giác abc, từ b và c kẻ bd và ce vuông với d (d và e thuộc d).CM
a, tam giác bda = tam giác aec
b, bd+ce=de
bài 8: cho tam giác abc vuông tại a có góc b 60 ab 5cm, tia pgiac góc b cắt ac tại d, kẻ de vuông với bc tại d.CM
a, tam giác abd= tam giác ebd
b, tam giác abe là tam giác đều
c, bc = ?
bài 9: cho tam giác abc cân tại a, kẻ bd vuông với ac ce vuông với ab ( d thuộc ac, e thuộc ab), o là giao điểm của bd và ce.CM
a, bd=ce
b,tam giác oeb= tam giác odc
c, ao là pgiacs góc bac
d, cho biết be=3cm, bc=5cm. BD=?
bài 10: cho tam giác abc vuông tại a, đg pgiac bd ( d thuộc ac) từ d kẻ dh vuông với bc tại h. CM
a, tam giác ade cân
b, góc dae= góc acd
c, từ b, c lẻ các đg thg lần lượt vuông góc với ad và a, cắt nhau tại o.CM: ao là đg trung trực của bc
Bạn nào trả lời được thì xin hãy giúp tớ luôn mai tớ phài nộp rồi nhưng tuần này nghỉ tết sức khỏe ko tốt ko đc đi đâu chơi chỉ ở nhà nằm nghỉ đc thôi. Bạn nào trả lời nhanh nhất tớ tích cho
2/
Ta có (x2 + 4) (x - 1) = 0
=> \(\orbr{\begin{cases}x^2+4=0\\x-1=0\end{cases}}\)=> \(\orbr{\begin{cases}x^2=4\\x=1\end{cases}}\)=> \(\orbr{\begin{cases}x=2\\x=1\end{cases}}\)
Thay x = 2 vào biểu thức B, ta có:
B = 3x2 + 8x - 1 = 3. 22 + 8.2 - 1 = 3.4 + 8.2 - 1 = 12 + 16 - 1 = 27
Thay x = 1 vào biểu thức B, ta có:
B = 3x2 + 8x - 1 = 3.12 + 8.1 - 1 = 3 + 8 - 1 = 11
Vậy khi (x2 + 4) (x - 1) = 0 thì giá trị của biểu thức B là 27 hoặc 11.
3/
a) Gọi Amin là GTNN của A.
Ta có: \(\left(x-1\right)^2\ge0\)với mọi gt của x
\(\left(y-1\right)^2\ge0\)với mọi gt của x
=> \(\left(x-1\right)^2+\left(y-1\right)^2\ge0\)với mọi gt của x
=> Amin = (x - 1)2 + (y - 1)2 = 0
=> \(\hept{\begin{cases}\left(x-1\right)^2=0\\\left(y-1\right)^2=0\end{cases}}\)=> \(\hept{\begin{cases}x-1=0\\y-1=0\end{cases}}\)=> \(\hept{\begin{cases}x=1\\y=1\end{cases}}\)
Vậy GTNN của biểu thức A bằng 0 khi x = 1 và y = 1.
b) Gọi Bmin là GTNN của B
Ta có \(\left|x-3\right|\ge0\)với mọi gt của x
\(y^2\ge0\)với mọi gt của x
=> \(\left|x-3\right|+y^2\ge0\)với mọi gt của x
=> \(\left|x-3\right|+y^2-10\ge-10\)với mọi gt của x
=> Bmin = |x - 3| + y2 - 10 = -10
=> |x - 3| + y2 = 0
=> \(\hept{\begin{cases}\left|x-3\right|=0\\y^2=0\end{cases}}\)=> \(\hept{\begin{cases}x-3=0\\y=0\end{cases}}\)=> \(\hept{\begin{cases}x=3\\y=0\end{cases}}\)
Vậy GTNN của biểu thức B bằng -10 khi x = 3 và y = 0.
Trong tam giác ABC vuông tại A có AC =3; AB =4. Khi đó cos B bằng