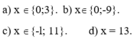a) x Î{0;3}.

b) xÎ{0;-9}.

c) x Î{-l; 11}.

d) x = 13.

`@` `\text {Ans}`

`\downarrow`

`1,`

`x^2 - 9 = 0`

`<=> x^2 = 0 + 9`

`<=> x^2 = 9`

`<=> x^2 = (+-3)^2`

`<=> x = +-3`

Vậy, `S = {3; -3}`

`2,`

`25 - x^2 = 0`

`<=> x^2 = 25 - 0`

`<=> x^2 = 25`

`<=> x^2 = (+-5)^2`

`<=> x = +-5`

Vậy,` S= {5; -5}`

`3,`

`-x^2 + 36 = 0`

`<=> -x^2 = 0 - 36`

`<=> -x^2 = -36`

`<=> x^2 = 36`

`<=> x^2 = (+-6)^2`

`<=> x = +-6`

Vậy, `S= {6; -6}`

`4,`

`4x^2 - 4 = 0`

`<=> 4x^2 = 0+4`

`<=> 4x^2 = 4`

`<=> x^2 = 4 \div 4`

`<=> x^2 = 1`

`<=> x^2 = (+-1)^2`

`<=> x = +-1`

Vậy, `S= {1; -1}`

`@` `\text {Kaizuu lv uuu}`

`(4x+1)(-x-9)=0`

\(< =>\left[{}\begin{matrix}4x+1=0\\-x-9=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}4x=-1\\-x=9\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=-\dfrac{1}{4}\\x=-9\end{matrix}\right.\)

`(4x+1)(-x-9)=0`

TH1: `4x+1=0`

`=>4x=-1`

`=>x=-1/4`

TH2: `-x-9=0`

`=>-x=9`

`=>x=-9`

Vậy `x\in{-1/4;-9}`

=>5x+25=0

=>5x=-25

hay x=-5

b: 

1: \(\Leftrightarrow2x\left(x+2\right)=0\)

=>x=0 hoặc x=-2

\(x.\left(x-\frac{1}{7}\right)\left(\frac{1}{9}+x\right)< 0\)

có 4 TH ( Trường hợp)

TH1: \(\hept{\begin{cases}x>0\\x-\frac{1}{7}>0\\\frac{1}{9}+x< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x>0\\x>\frac{1}{7}\\x< -\frac{1}{9}\end{cases}}}\)( vô lí)

TH2:\(\hept{\begin{cases}x>0\\x-\frac{1}{7}< 0\\\frac{1}{9}+x>0\end{cases}\Leftrightarrow\hept{\begin{cases}x>0\\x< \frac{1}{7}\\x>-\frac{1}{9}\end{cases}\Leftrightarrow}0< x< \frac{1}{7}}\)

TH3:\(\hept{\begin{cases}x< 0\\x-\frac{1}{7}>0\\\frac{1}{9}+x>0\end{cases}\Leftrightarrow\hept{\begin{cases}x< 0\\x>\frac{1}{7}\\x>-\frac{1}{9}\end{cases}}}\)(vô lí )

TH4:\(\hept{\begin{cases}x< 0\\x+\frac{1}{7}< 0\\\frac{1}{9}-x< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x< 0\\x< -\frac{1}{7}\\x>\frac{1}{9}\end{cases}}}\)(vô lí)

KL: 0<x<1/7 

b) \(\frac{\left(4-x\right)}{2x}-\frac{1}{5}>0\)đk: \(x\ne0\)

<=>  \(\left(4-x\right).5-2x.1>0\)

<=>   \(20-5x-2x>0\)

<=>  \(20-7x>0\)

<=> \(20>7x\Leftrightarrow x< \frac{20}{7}\)

a)4x²-9=0

⇔ (2x-3)(2x+3)=0

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)

b)(x+5)²-(x-1)²=0

⇔ (x+5-x+1)(x+5+x-1)=0

⇔ 12(x+2)=0

⇔ x=-2

c)x²-6x-7=0

⇔ x²-7x+x-7=0

⇔ x(x-7)+(x-7)=0

⇔ (x-7)(x+1)=0

\(\Leftrightarrow\left\{{}\begin{matrix}x=7\\x=-1\end{matrix}\right.\)

d)(x+1)²-(2x-1)²=0

⇔ (x+1-2x+1)(x+1+2x-1)=0

⇔3x(2-x)=0

\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

a, 4x² - 9 = 0

<=> 4x² = 9

<=> x² = \(\dfrac{9}{4}\) => x = \(\sqrt{\dfrac{9}{4}}\)

b, (x + 5 )² - ( x - 1 )² = 0

<=> ( x+5-x+1 )(x+5+x-1) = 0

<=> 6(2x+4) = 0

<=> 12x+24=0

<=> 12x = -24

<=> x = -2

c, x²-6x-7=0

<=> x²+x-7x-7=0

<=> x(x+1)-7(x+1)=0

<=> (x-7)(x+1)=0

=> x+7=0 hoặc x+1=0

+ x-7=0 => x=7

+ x+1=0 => x=-1

d, \(\left(x+1\right)^2-\left(2x-1\right)^2=0\)

<=> \(\left(x+1-2x+1\right)\left(x+1+2x-1\right)=0\)

<=> (-x+2).3x=0

=> x=0 hoặc (-x+2).3=0

+ (-x+2).3=0 => -3x+6=0 => x=-2

b) (x +5)² -(x -1)²=0

<=> [(x +5) -(x -1)][(x +5) +(x -1)]=0

<=> (x +5 -x +1)(x +5 +x -1)=0

<=> 6(2x+4)=0 <=>12(x +2)=0

=> x +2=0=> x=-2

vậy x= -2

c) x² -6x -7=0

<=> x² -7x +x -7=0

<=> (x² +x)( -7x -7)=0

<=> x(x +1).-7(x +1)=0

<=> (x +1)(x -7)=0

<=> \(\left\{{}\begin{matrix}x+1=0\\x-7=0\end{matrix}\right.< =>\left\{{}\begin{matrix}x=-1\\x=7\end{matrix}\right.\)

Vậy S={-1; 7}

d) (x +1)² -(2x -1)²=0

<=> [(x -1)-(2x -1)][(x -1)+(2x -1)]=0

<=> (x -1 -2x +1)(x -1 +2x -1)=0

<=> (x -2x)(3x -2)<=> -x(3x -2)=0

<=> \(\left\{{}\begin{matrix}-x=0\\3x-2=0\end{matrix}\right.< =>\left\{{}\begin{matrix}x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)

Vậy S={0; \(\dfrac{2}{3}\)}

a, \(\left(x-1\right).\left(x+2\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-1=0\\x+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)

b, \(\left(2x-4\right).\left(3x+9\right)=0\\ \Rightarrow\left[{}\begin{matrix}2x-4=0\\3x+9=0\end{matrix}\right.\left[{}\begin{matrix}2x=4\\3x=-9\end{matrix}\right.\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)

a) TH₁: x-1=0 => x=1

     TH₂: x+2=0 => x=-2

b) TH₁: 2x-4=0 <=> 2x= 4 <=> x=2

     TH₂: 3x+9=0 <=> 3x=-9 <=> x= -3

a) ( x - 1) . ( x + 2 ) = 0 

=> x - 1 = 0 => x = 1

     x + 2 = 0     x = -2 

vậy x ϵ { 1; -2 }

b) ( 2x - 4 ) . ( 3x + 9 ) = 0

=> 2x - 4  = 0   => 2x = 4  => x = 2

     3x + 9 = 0        3x = -9      x = -3

vậy x ϵ { 2 ; -3 {

P/S : phần mình suy ra thì bn đóng ngoặc vuông to rồi mới ghi phép tính nhé!