Phương trình log2( 5x - 1) log2( 2.5x - 2) = 2 có hai nghiệm phân biệt
Tỉ số x 1 x 2 gần với giá trị nào sau đây nhất, biết rằng x1 > x2 > 0
A. 4
B. 3
C. 5
D. 2
Tìm tất cả các giá trị thực của tham số m để bất phương trình log2( 5x - 1) .log2)( 2.5x - 2) > m - 1 có nghiệm x ≥ 1?
A. m ≥ 7
B. m > 7
C. m ≤ 7
D. m < 7
Số các giá trị nguyên của tham số m để phương trình log 2 ( x - 1 ) = log 2 ( m x - 8 ) có hai nghiệm thực phân biệt là :
A. 3
B. 4
C. 5
D. vô số
Biết rằng phương trình log 2 x - log x 64 = 1 có hai nghiệm phân biệt. Khi đó tích hai nghiệm này bằng bao nhiêu?
A. 2.
B. 1.
C. 1 4
D. 1 2
Tìm số nghiệm của phương trình log2 x + log2 (x -1) = 2
A. 0
B. 1
C. 3
D. 2
Có bao nhiêu giá trị nguyên của tham số m để phương trình log 2 ( x 2 - 2 x + 5 ) - m . log x 2 - 2 x + 5 2 = 5 có hai nghiệm phân biệt là nghiệm của bất phương trình log 2017 ( x + 1 ) - log 2017 ( x - 1 ) > log 2017 4
A. 0
B. 1
C. 3
D. 2
Tìm tập nghiệm của phương trình log2(x - 2) + log2(x+1) = 2
![]()
![]()
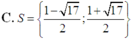
![]()
Tập nghiệm của bất phương trình log 2 ( x + 1 ) - 2 log 4 ( 5 - x ) < 1 - log 2 ( x - 2 ) là
A. (3;5)
B. (2;3)
C. (2;5)
D. (-4;3)
Tìm các giá trị của tham msố để phương trình log 2 ( m x ) log 2 ( x + 1 ) = 2 có nghiệm duy nhất
A. m < 0
B. m > 4
C. m < 0 ∪ m = 4
D. m < 0 ∪ m ≥ 4
Tính tổng tất cả các nghiệm của phương trình: \(\dfrac{1}{2}\).log2(x+3) = log2(x+1) + x2 - x - 4 + 2\(\sqrt{x+3}\)
ĐKXĐ: \(x>-1\)
Bước quan trọng nhất là tách hàm
\(\Leftrightarrow log_2\sqrt{x+3}-2\sqrt{x+3}+\left(x+3\right)=log_2\left(x+1\right)-2\left(x+1\right)+\left(x+1\right)^2\)
Đến đây coi như xong \(\Rightarrow\sqrt{x+3}=x+1\Rightarrow x=1\)