Gọi x 0 là nghiệm của phương trình 2.(x – 3) + 5x(x – 1) = 5 x 2 . Chọn khẳng định đúng.
A. x 0 > 0
B. x 0 < -2
C. x 0 > -2
D. x 0 > - 3
Số x 0 được gọi là nghiệm của phương trình A(x) = B(x) khi
A. A( x 0 ) < B( x 0 )
B. A( x 0 ) > B( x 0 )
C. A( x 0 ) = -B( x 0 )
D. A( x 0 ) = B( x 0 )
Giá x 0 thỏa mãn A( x 0 ) = B( x 0 ) được gọi là nghiệm của phương trình A(x) = B(x)
Đáp án cần chọn là: D
Gọi x 0 là nghiệm của phương trình 3(x – 2) – 2x(x + 1) = 3 – 2 x 2 . Chọn khẳng định đúng.
A. x 0 là số nguyên âm
B. x 0 là số nguyên dương
C. x 0 không là số nguyên
D. x 0 là số vô tỉ
Gọi (x; y) là nghiệm nguyên dương nhỏ nhất của phương trình −4x + 3y = 8. Tính x + y
A. 5
B. 6
C. 7
D.
Ta có −4x + 3y = 8 ⇔ y = 4 x + 8 3 ⇔ y = x + x + 8 3
Đặt x + 8 3 = t ⇒ x = 3t – 8 ⇒ y = 3t – 8 + t ⇒ y = 4t – 8 ( )
Nên nghiệm nguyên của phương trình là x = 3 t − 8 y = 4 t − 8 t ∈ ℤ
Vì x, y nguyên dương nên x > 0 y > 0 ⇒ 3 t − 8 > 0 4 t − 8 > 0 ⇒ t > 8 3 t > 2 ⇒ t > 8 3
mà t ∈ ℤ ⇒ t ≥ 3
Nghiệm nguyên dương nhỏ nhất của phương trình là x = 3.3 − 8 y = 4.3 − 8 ⇔ x = 1 y = 4
⇒ x + y = 5
Đáp án: A
Phương trình log3( 3x - 6) = 3 - x có nghiệm duy nhất x0. Biết rằng x0 cũng là nghiệm của phương trình log3( x + 7a) = 2log2x. Mệnh đề nào dưới đây đúng ?
A. 1 < a < 2
B. 0 < a < 1
C. 2 < a < 4
D. a ∈ 1 2 ; 2
Chọn D.
Phương trình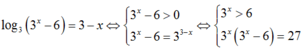 
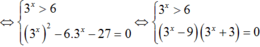
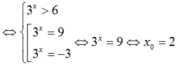
Mà x0 là nghiệm của phương trình log3( x + 7a) = 2log2x nên suy ra
log3( x + 7a) = 2log2x tương đương log3( x +7a) = 2
do đó; 7a + 2 = 32
suy ra a = 1.
cho bất phương trình \(f\left(x\right)\le g\left(x\right),x_0\) là một nghiệm của bất phương trình \(f\left(x\right)\le g\left(x\right)\) nếu:
A. f(x0)=g(x0) đúng
B. f(x0) >= g(xo) đúng
C. f(x0) <= g(x0) sai
D. f(x0) > g(x0) đúng
Gọi (x; y) là nghiệm nguyên dương nhỏ nhất của phương trình 6x − 7y = 5. Tính x – y
A. 2
B. 3
C. 1
D. −1
Ta có 6x – 7y = 5 ⇔ x = 7 y + 5 6 ⇔ x = y + y + 5 6
Đặt y + 5 6 = t t ∈ ℤ ⇒ y = 6t – 5 = 6 ⇒ x = y + y + 5 6 = 6t – 5 + t = 7t – 5
Nên nghiệm nguyên của phương trình là x = 7 t − 5 y = 6 t − 5 t ∈ ℤ
Vì x, y nguyên dương nên x > 0 y > 0 ⇒ 7 t − 5 > 0 6 t − 5 > 0 ⇒ t > 5 7 t > 5 6 ⇒ t > 5 7
mà t ∈ ℤ ⇒ t ≥ 1
Do đó nghiệm nguyên dương nhỏ nhất của phương trình có được khi t = 1
⇒ x = 7.1 − 5 y = 6.1 − 5 ⇒ x = 2 y = 1 ⇒ x − y = 1
Đáp án: C
Gọi x 0 là một nghiệm của phương trình 5x – 12 = 4 - 3x. Hỏi x0 còn là nghiệm của phương trình nào dưới đây?
A. 2x – 4 = 0
B. -x – 2 = 0
C. x 2 + 4 = 0
D. 9 – x 2 = -5
giả sử (x0,y0) là nghiệm của hệ phương trình \(\left\{{}\begin{matrix}x^2+y^2=25\\x+y-xy=-5\end{matrix}\right.\)
