Cho hai góc α và β với α + β = 90 ° . Tính giá trị của biểu thức P = cos α cos β − sin β sin α .
A.P = 0
B. P = 1
C. P = -1
D. P = 2
Hai góc α và β phụ nhau nên sin α = cos β ; cos α = sin β .
Do đó, P = cos α cos β − sin β sin α = cos α sin α − cos α sin α = 0 .
Chọn A.
Cho hai góc α và β với α + β = 180 ° . Tính giá trị của biểu thức P = cos α cos β − sin β sin α .
A.P = 0
B. P = 1
C . P = -1
D. P = 2
Hai góc α và β bù nhau nên sin α = sin β ; cos α = − cos β .
Do đó P = cos α cos β − sin β sin α = − cos 2 α − sin 2 α = − sin 2 α + cos 2 α = − 1 .
Chọn C.
Cho hai góc phụ nhau α và β . Tính giá trị của biểu thức P = sinα.cosβ + sinβ.cosα.
A. 0
B. 1
C. -1
D. 2
Chọn B.
Hai góc α và β phụ nhau nên sinα = cosβ và cosα = sinβ.
Do đó, P = sinα.cosβ+ sinβ.cosα = sin2α + cos2α = 1.
Cho hai góc bù nhau α và β. Tính giá trị của biểu thức P= cosα.cosβ- sinα.sinβ.
A. P = 0
B. P = 1
C. P = -1
D. P = 2
Chọn C.
Hai góc α và β bù nhau nên sinα = sinβ và cosα = - cosβ.
Do đó P = cosα.cosβ- sinα.sinβ.
= -cos2α – sin2α = -1
Cho hai góc phụ nhau α và β. Tính giá trị của biểu thức A = cosα.cosβ - sinα.sinβ.
A. 0
B. 1
C. -1
D. 2
Chọn A.
Hai góc α và β phụ nhau nên sinα = cosβ và cosα = sinβ.
Do đó, A = cosα.cosβ - sinα.sinβ = cosαsinα - cosα.sinα = 0.
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(10;6;-2),B(5;10;-9) và mặt phẳng (P):2x+2y+z-12=0. Gọi M(a;b;c) là điểm di động trên mặt phẳng (P) sao cho MA, MB tạo với m.t ph.ng (P) các góc α , β thỏa mãn α + β = 90 ° . Khi biểu thức T=4MA+MB đạt giá trị nhỏ nhất. Giá trị của biểu thức a+b+c bằng
A. 15.
B. 3.
C. 5.
D. 13.
Cho các góc α, β nhọn và α < β.
CMR : cos(β – α) = cos β. cos α + sin β.sin α .
Tìm đẳng thức đúng
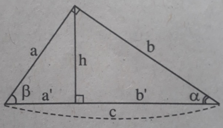
A. sin α = sin β B. sin α = cos β
C. sin α = tg β D. sin α = cotg β
Cho α , β thỏa mãn sin α + sin β = 2 2 ; cos α + cos β = 6 2 . Tính cos α - β .
A. cos α - β = 0
B. cos α - β = 2 2
C. cos α - β = 3 2
D. cos α - β = 1 2
