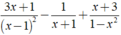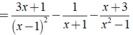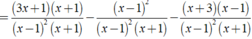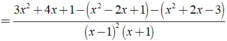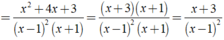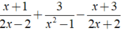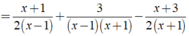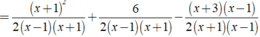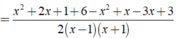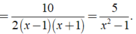b: \(\dfrac{xy}{2x-y}-\dfrac{2x^2}{y-2x}=\dfrac{xy}{2x-y}+\dfrac{2x^2}{2x-y}=\dfrac{xy+2x^2}{2x-y}\)

b: \(\dfrac{3x^2-x}{x-1}+\dfrac{x+2}{1-x}+\dfrac{3-2x^2}{x-1}\)

\(=\dfrac{3x^2-x-x-2+3-2x^2}{x-1}\)

\(=\dfrac{x^2-2x+1}{x-1}=x-1\)

Bài 1: 

b: \(=\dfrac{x+3-4-x}{x-2}=\dfrac{-1}{x-2}\)

Bài 2: 

a: \(=\dfrac{x+1}{2\left(x+3\right)}+\dfrac{2x+3}{x\left(x+3\right)}\)

\(=\dfrac{x^2+x+4x+6}{2x\left(x+3\right)}=\dfrac{x^2+5x+6}{2x\left(x+3\right)}=\dfrac{x+2}{2x}\)

d: \(=\dfrac{3}{2x^2y}+\dfrac{5}{xy^2}+\dfrac{x}{y^3}\)

\(=\dfrac{3y^2+10xy+2x^3}{2x^2y^3}\)

e: \(=\dfrac{x^2+2xy+x^2-2xy-4xy}{\left(x+2y\right)\left(x-2y\right)}=\dfrac{2x^2-4xy}{\left(x+2y\right)\cdot\left(x-2y\right)}=\dfrac{2x}{x+2y}\)

\(=\left(\dfrac{1}{x\left(x+1\right)}+\dfrac{x-2}{x+1}\right):\left(\dfrac{1}{x}+x-2\right)\)

\(=\dfrac{x^2-2x+1}{x\left(x+1\right)}:\dfrac{x^2-2x+1}{x}\)

\(=\dfrac{1}{x+1}\)

\(-3ab.\left(a^2-3b\right)\)

\(=-3a^3b+9ab^2\)

\(\left(x^2-2xy+y^2\right)\left(x-2y\right)\)

\(=x^3-2x^2y+xy^2-2x^2y+4xy^2-2y^3\)

\(=x^3-4x^2y+5xy^2-2y^3\)

a) \(-3ab.\left(a^2-3b\right)=-3ab.a^2+3ab.3b=-3a^3b+9ab^2\)

b) \(\left(x^2-2xy+y^2\right).\left(x-2y\right)=\left(x-2y\right).x^2-\left(x-2y\right).2xy+\left(x-2y\right).y^2\)

\(=xx^2-2yx^2-2xyx+2xy2y+xy^2-2yy^2\)

\(=x^3-\left(2yx^2+2yx^2\right)+\left(4xy^2+xy^2\right)-2y^3\)

\(=x^3-4yx^2+5xy^2-2y^3\)

mk chỉ có thể thu gọn đc thôi, mk ko tính đc đâu!

a.

\(\dfrac{x^3}{x-1}-\dfrac{x^2}{x+1}-\dfrac{1}{x-1}+\dfrac{1}{x+1}=\dfrac{x^3-1}{x-1}-\dfrac{x^2-1}{x+1}\)

\(=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x-1}-\dfrac{\left(x-1\right)\left(x+1\right)}{x+1}\)

\(=x^2+x+1-\left(x-1\right)=x^2+2\)

b.

\(\dfrac{x+y}{2\left(x-y\right)}-\dfrac{x-y}{2\left(x+y\right)}+\dfrac{2y^2}{x^2-y^2}\)

\(=\dfrac{\left(x+y\right)^2}{2\left(x-y\right)\left(x+y\right)}-\dfrac{\left(x-y\right)^2}{2\left(x-y\right)\left(x+y\right)}+\dfrac{4y^2}{2\left(x-y\right)\left(x+y\right)}\)

\(=\dfrac{\left(x+y\right)^2-\left(x-y\right)^2+4y^2}{2\left(x-y\right)\left(x+y\right)}\)

\(=\dfrac{4xy+4y^2}{2\left(x-y\right)\left(x+y\right)}=\dfrac{4y\left(x+y\right)}{2\left(x-y\right)\left(x+y\right)}\)

\(=\dfrac{2y}{x-y}\)

c.

\(\dfrac{x+5}{2x-4}.\dfrac{4-2x}{x+2}=\dfrac{x+5}{2x-4}.\dfrac{-\left(2x-4\right)}{x+2}=-\dfrac{x+5}{x+2}\)

d.

\(\dfrac{8}{x^2+2x-3}+\dfrac{2}{x+3}+\dfrac{1}{x-1}=\dfrac{8}{\left(x-1\right)\left(x+3\right)}+\dfrac{2\left(x-1\right)}{\left(x-1\right)\left(x+3\right)}+\dfrac{x+3}{\left(x-1\right)\left(x+3\right)}\)

\(=\dfrac{8+2\left(x-1\right)+x+3}{\left(x-1\right)\left(x+3\right)}=\dfrac{3x+9}{\left(x-1\right)\left(x+3\right)}\)

\(=\dfrac{3\left(x+3\right)}{\left(x-1\right)\left(x+3\right)}=\dfrac{3}{x-1}\)

Bài 2:

1: \(A=\left(x+2\right)\left(x^2-2x+4\right)+2\left(x+1\right)\left(1-x\right)\)

\(=\left(x+2\right)\left(x^2-x\cdot2+2^2\right)-2\left(x+1\right)\left(x-1\right)\)

\(=x^3+2^3-2\left(x^2-1\right)\)

\(=x^3+8-2x^2+2=x^3-2x^2+10\)

\(B=\left(2x-y\right)^2-2\left(4x^2-y^2\right)+\left(2x+y\right)^2+4\left(y+2\right)\)

\(=\left(2x-y\right)^2-2\cdot\left(2x-y\right)\left(2x+y\right)+\left(2x+y\right)^2+4\left(y+2\right)\)

\(=\left(2x-y-2x-y\right)^2+4\left(y+2\right)\)

\(=\left(-2y\right)^2+4\left(y+2\right)\)

\(=4y^2+4y+8\)

2: Khi x=2 thì \(A=2^3-2\cdot2^2+10=8-8+10=10\)

3: \(B=4y^2+4y+8\)

\(=4y^2+4y+1+7\)

\(=\left(2y+1\right)^2+7>=7>0\forall y\)

=>B luôn dương với mọi y

Bài 1:

5: \(x^2\left(x-y+1\right)+\left(x^2-1\right)\left(x+y\right)\)

\(=x^3-x^2y+x^2+x^3+x^2y-x-y\)

\(=2x^3-x+x^2-y\)

6: \(\left(3x-5\right)\left(2x+11\right)-6\left(x+7\right)^2\)

\(=6x^2+33x-10x-55-6\left(x^2+14x+49\right)\)

\(=6x^2+23x-55-6x^2-84x-294\)

=-61x-349

Ta có: 

Ta có: 

MTC = (x - y)(x² + xy + y²)

\(\dfrac{1}{x-y}-\dfrac{3xy}{x^3-y^3}+\dfrac{x-y}{x^2+xy+y^2}\)

\(=\dfrac{x^2+xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}-\dfrac{3xy}{\left(x-y\right)\left(x^2+xy+y^2\right)}+\dfrac{\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)

\(=\dfrac{x^2+xy+y^2-3xy+\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)

\(=\dfrac{x^2+xy+y^2-3xy+x^2-2xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)

\(=\dfrac{2x^2-4xy+2y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)

\(=\dfrac{2\left(x^2-2xy+y^2\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)

\(=\dfrac{2\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)

\(=\dfrac{2\left(x-y\right)}{x^2+xy+y^2}\)

1/x-y-3xy/x^3-y^3+x-y/x^2+xy+y^2

=1/x-y+-3xy/(x-y)(x^2+xy+y^2)+x-y/x^2+xy+y^2

=x^2+xy+y^2/(x-y)(x^2+xy+y^2)+-3xy/(x-y)(x^2+xy+y^2)+x^2-2xy+y^2/(x-y)(x^2+xy+y^2)

=x^2+xy+y^2-3xy+x^2-2xy-y^2/(x-y)(x^2+xy+y^2)

=2x^2-5xy/(x-y)(x^2+xy+y^2)

MTC = (x - y)(x² + xy + y²)

\(\dfrac{1}{x-y}-\dfrac{3xy}{x^3-y^3}+\dfrac{x-y}{x^2+xy+y^2}\)

\(=\dfrac{x^2+xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}-\dfrac{3xy}{\left(x-y\right)\left(x^2+xy+y^2\right)}+\dfrac{\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)

\(=\dfrac{x^2+xy+y^2-3xy+\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)

\(=\dfrac{x^2+xy+y^2-3xy+x^2-2xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)

\(=\dfrac{2x^2-4xy+2y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)

\(=\dfrac{2\left(x^2-2xy+y^2\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)

\(=\dfrac{2\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)

\(=\dfrac{2\left(x-y\right)}{x^2+xy+y^2}\)