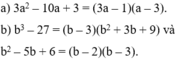Cho đẳng thức a − 2 b 27 a 3 + b 3 . B = a 2 + 4 ab + 4 b 2 9 a 2 − 3 ab + b 2 với a ≠ − 1 3 b và a ≠ 2 b . Tìm B.

Những câu hỏi liên quan
Bài 1: Phân tích đa thức thành nhân tử ( phương pháp dùng hằng đẳng thức)
(a-2b)^2-4b^2 (a-b)^2-c^2 (a+b)^2-4 (a+3b)^2-9b^2
(x-3)^3-27 (x+1)^3-125
Bài 1: Phân tích đa thức thành nhân tử ( phương pháp dùng hằng đẳng thức)
(a-2b)^2-4b^2 (a-b)^2-c^2 (a+b)^2-4 (a+3b)^2-9b^2
(x-3)^3-27 (x+1)^3-125
Chứng minh các đẳng thức sau:a)
3
a
2
−
10
a
+
3
2
(
a
−
3
)
3
2
a
−
1
2
với a
≠
3;...
Đọc tiếp
Chứng minh các đẳng thức sau:
a) 3 a 2 − 10 a + 3 2 ( a − 3 ) = 3 2 a − 1 2 với a ≠ 3;
b) b 2 + 3 b + 9 b 3 − 27 = b − 2 b 2 − 5 b + 6 với b ≠ 2 và b ≠ 3.
Bất đẳng thức sau đúng hay sai : Cho a,b,c >0 và \(\sum { { a }^{ 2 } } \)=3 thì : \(4\sum { \frac { a }{ \sqrt { { a }^{ 2 }+3{ b }^{ 2 } } } \ge \frac { 3{ (a+b+c) }^{ 2 }+27 }{ 3\sqrt { 3(a+b+c) } } } \)
sử dụng hằng đẳng thức đabg nhớ tinh nhanh
a) (27/8x^3 -1):(3/2x-1)
b) (8x^3 +36x^2 +54x +27):(2x +3)
a, \(\dfrac{27}{8x^3-1}:\dfrac{3}{2x-1}\)
\(=\dfrac{27}{\left(2x-1\right)\left(4x^2+2x+1\right)}.\dfrac{2x-1}{3}\)
\(=\dfrac{9}{4x^2+2x+1}\)
b, \(\dfrac{8x^3+36x^2+54x+27}{2x+3}=\dfrac{\left(2x+3\right)^3}{2x+3}=\left(2x+3\right)^2\)
Đúng 0
Bình luận (0)
1) So sánh :
a) 23-2√19/3 và 27
b) √(3√3) va √(2√2)
c) √(4-√7) - √(4+√7) - √2 và số 0
2) C/m đẳng thức: lAl + lBl>= lA+Bl. Đẳng thức xảy ra khi nào.
Lập tất cả các tỉ lệ thức có thể từ đẳng thức sau: a) 7 × -28 = -49 x 4 b)-3 x 20 = 4 × -15 c) - 2× -27 = -9 x -6
a: 7/-49=4/-28
7/4=-49/-28
-49/7=-28/4
4/7=-28/-49
b: -3/4=-15/20
-3/-15=4/20
4/-3=20/-15
-15/-3=20/4
c: -2/-9=-6/-27
-2/-6=-9/-27
-9/-2=-27/-6
-6/-2=-27/-9
Đúng 2
Bình luận (0)
Chứng minh các đẳng thức sau:
a.\(\dfrac{3a^2-10a+3}{2\left(a-3\right)}=\dfrac{3}{2}a-\dfrac{1}{2}\)với a≠3
b.\(\dfrac{b^2+3b+9}{b^3-27}=\dfrac{b-2}{b^2-5b+6}với\) b≠2 và b≠3
giúp mik với mik đang cần gấp
a) Ta có: \(\dfrac{3a^2-10a+3}{2\left(a-3\right)}\)
\(=\dfrac{3a^2-9a-a+3}{2\left(a-3\right)}\)
\(=\dfrac{3a\left(a-3\right)-\left(a-3\right)}{2\left(a-3\right)}\)
\(=\dfrac{\left(a-3\right)\left(3a-1\right)}{2\left(a-3\right)}\)
\(=\dfrac{3a-1}{2}\)
\(=\dfrac{3}{2}a-\dfrac{1}{2}\)(đpcm)
b) Ta có: \(\dfrac{b^2+3b+9}{b^3-27}\)\(=\dfrac{b^2+3b+9}{\left(b-3\right)\left(b^2+3b+9\right)}\)
\(=\dfrac{1}{b-3}\)
\(=\dfrac{b-2}{\left(b-3\right)\left(b-2\right)}\)
\(=\dfrac{b-2}{b^2-5b+6}\)(đpcm)
Đúng 2
Bình luận (1)
Chứng minh các đẳng thức sau (với n∈N∗n∈N∗)
a) 2+5+8+...+(3n−1)=n(3n+1)22+5+8+...+(3n−1)=n(3n+1)2;
b) 3+9+27+...+3n=12(3n+1−3)3+9+27+...+3n=12(3n+1−3).
tham khảo:
\(a) 2+5+8+...+(3n−1)=n(3n+1)2 (1) Đặt Sn=2+5+8+...+(3n−1) Với n=1 ta có: S1=2=1(3.1+1)2 Giả sử (1) đúng với n=k(k≥1), tức là Sk=2+5+8+...+(3k−1)=k(3k+1)2 Ta chứng minh (1) đúng với n=k+1 hay Sk+1=(k+1)(3k+4)2 Thật vậy ta có: Sk+1=2+5+8+...+(3k−1)+[3(k+1)−1]=Sk+3k+2=k(3k+1)2+3k+2=3k2+k+6k+42=3k2+7k+42=(k+1)(3k+4)2 Vậy (1) đúng với mọi k≥1 hay (1) đúng với mọi n∈N∗ b) 3+9+27+...+3n=12(3n+1−3) (2) Đặt Sn=3+9+27+...+3n=12(3n+1−3) Với n=1, ta có: S1=3=12(32−3) (hệ thức đúng) Giả sử (2) đúng với n=k(k≥1) tức là Sk=3+9+27+...+3k=12(3k+1−3) Ta chứng minh (2) đúng với n=k+1, tức là chứng minh Sk+1=12(3k+2−3) Thật vậy, ta có: Sk+1=3+9+27+...+3k+1=Sk+3k+1=12(3k+1−3)+3k+1=32.3k+1−32=12(3k+2−3)(đpcm) Vậy (2) đúng với mọi k≥1 hay đúng với mọi n∈N∗\)
Đúng 0
Bình luận (0)
Bài 1: lập tất cả các tỉ lệ thức có thể được từ các đẳng thức sau:A) 7.(-28) (-49) . 4B) 0,36 . 4,25 0,9 . 1,7Bài 2: lập tất cả các tỉ lệ thức có thể được từ các đẳng thức sau:6 : (-27) 6 : (-27) (-6frac{1}{2} ) : 29frac{1}{4}Bài 3: lập tất cả các tỉ lệ thức có thể được từ các đẳng thức sau:5 ; 25 ; 125 ; 625
Đọc tiếp
Bài 1: lập tất cả các tỉ lệ thức có thể được từ các đẳng thức sau:
A) 7.(-28) = (-49) . 4
B) 0,36 . 4,25 = 0,9 . 1,7
Bài 2: lập tất cả các tỉ lệ thức có thể được từ các đẳng thức sau:
6 : (-27) = 6 : (-27) = (\(-6\frac{1}{2}\) ) : \(29\frac{1}{4}\)
Bài 3: lập tất cả các tỉ lệ thức có thể được từ các đẳng thức sau:
5 ; 25 ; 125 ; 625
\(1.\)
\(a,\)
\(7.\left(-28\right)=\left(-49\right).4\)
Ta có : \(\frac{7}{-49}=\frac{4}{-28}\) \(\frac{-28}{4}=\frac{-49}{7}\)
\(\frac{7}{4}=\frac{-49}{-28}\) \(\frac{-28}{-49}=\frac{4}{7}\)
\(b,\)
\(0,36.4,25=0,9.1,7\)
Ta có : \(\frac{0,36}{0,9}=\frac{1,7}{4,25}\) \(\frac{0,36}{1,7}=\frac{0,9}{4,25}\)
\(\frac{4,25}{0,9}=\frac{1,7}{0,36}\) \(\frac{4,25}{1,7}=\frac{0,9}{0,36}\)
Đúng 0
Bình luận (0)