Đáp án A

Ta có:

  B A → = − 6 ; − 7 ; − 3

B C → = − m − 4 ; − m − 11 ; m + 7

Mặt khác: B A → . B C → = 0  nên m = − 4 .

CÓ: \(a^2+b^2=c^2.\)Nên ta có:
\(P=\frac{\left(a+b\right)\left(a+\sqrt{a^2+b^2}\right)\left(b+\sqrt{a^2+b^2}\right)}{ab\sqrt{a^2+b^2}}\)
\(=\frac{a+b}{\sqrt{a^2+b^2}}.\frac{a+\sqrt{a^2+b^2}}{a}.\frac{b+\sqrt{a^2+b^2}}{b}\)
\(=\left(\sqrt{\frac{a^2}{a^2+b^2}}+\sqrt{\frac{b^2}{a^2+b^2}}\right).\left(1+\sqrt{\frac{a^2+b^2}{a^2}}\right)\left(1+\sqrt{\frac{a^2+b^2}{a^2}}\right)\).
Đặt: \(x^2=\frac{a^2}{a^2+b^2};y^2=\frac{b^2}{a^2+b^2}\Rightarrow x^2+y^2=1\). Ta có:
\(P=\left(x+y\right)\left(1+\frac{1}{x}\right)\left(1+\frac{1}{y}\right)\)
\(=x+y+\frac{1}{x}+\frac{1}{y}+\frac{x}{y}+\frac{y}{x}+2\)\(\ge4\sqrt{x.y.\frac{1}{x}.\frac{1}{y}.\frac{x}{y}.\frac{y}{x}}+2=6.\)

Vậy GTNN của P = 6.Dấu bằng xảy ra khi x = y =1 hay tam giác ABC vuông cân.

Min = 6

\(B=\frac{1}{4}\left(a^2b^2\right)2ab\) tại a = 1, b = |2|

\(B=\frac{1}{4}\left(1^2.2^2\right)2.1.2\)

\(B=\frac{1}{4}.4.2.1.2\)

\(B=4\)

Vì tam giác ABC vuông tại A nên:   A B → . A C → = 0

A B → . B C → = A B → . A C → − A B → = A B → . A C → − A B → 2 = 0 − A B → 2 = − a 2

Chọn C.

Vì tam giác ABC vuông tại A nên: A B → . A C → = 0

A C → . B C → = A C → . A C → − A B → = A C → 2 −   A C → . A B → = A C 2 − 0 = a 2

Chọn  B.

Gọi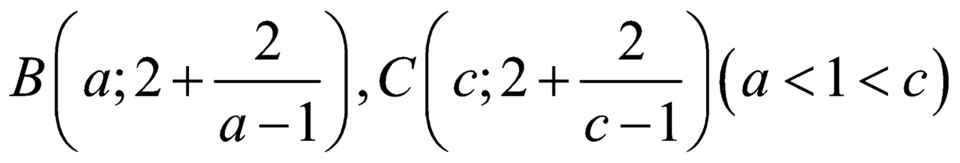  

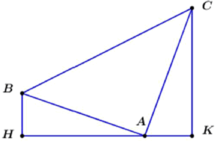
Gọi H, K lần lượt là hình chiếu của B, C trên trục  

vuông cân

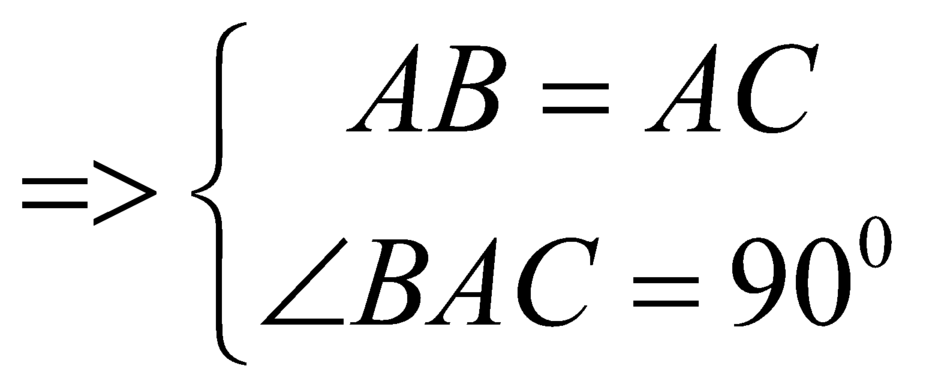
Ta có:

Mà: 

Xét và ta có:

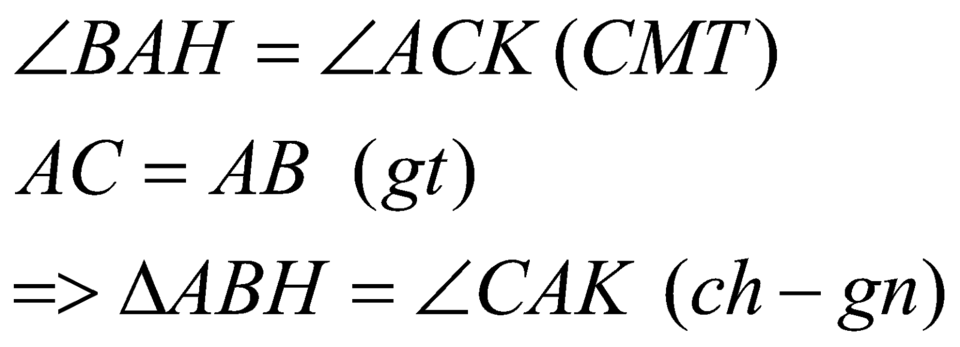
(các cạnh tương ứng bằng nhau)

Ta có: 

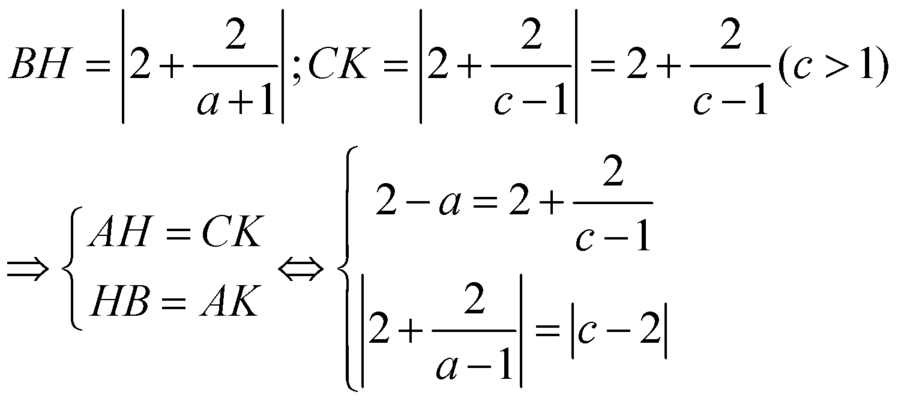
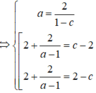
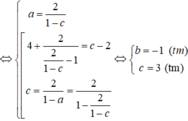
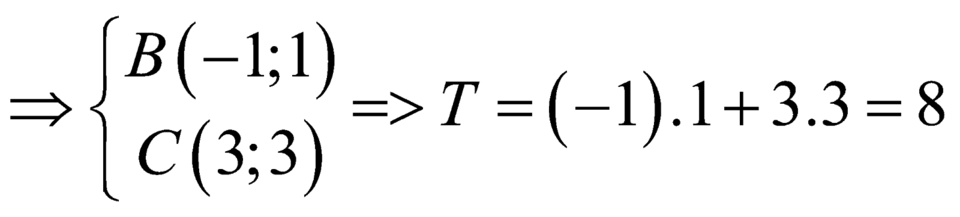
Chọn D.

Câu 1:

a: \(A=15\sqrt{4a}+\sqrt{a}-\sqrt{25a}\)

\(=15\cdot2\sqrt{a}+\sqrt{a}-5\sqrt{a}\)

\(=30\sqrt{a}-4\sqrt{a}=26\sqrt{a}\)

b: Sửa đề: Khi a=100

Thay a=100 vào A, ta được:

\(A=26\cdot\sqrt{100}=26\cdot10=260\)