Trong mặt phẳng tọa độ Oxy, cho bốn điểm A( 7; -3); B( 8; 4); C ( 1; 5) và D(0; -2). Khẳng định nào sau đây đúng?
A. A C → ⊥ C B → .
B. Tam giác ABC đều.
C. Tứ giác ABCD là hình vuông.
D. Tứ giác ABCD không nội tiếp đường tròn.
Trên mặt phẳng tọa độ Oxy cho bốn điểm: A(7; -3), B(8; 4), C(1; 5), D(0; –2). Chứng minh rằng tứ giác ABCD là hình vuông.
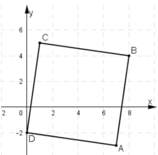
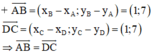
⇒ ABCD là hình bình hành.
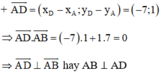
⇒ hình bình hành ABCD là hình chữ nhật.
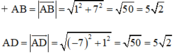
⇒ AB = AD ⇒ Hình chữ nhật ABCD là hình vuông (ĐPCM).
Trên mặt phẳng tọa độ Oxy cho bốn điểm A, B, C, D có tọa độ nguyên như sau:
A(4;5) B(1;-1) C(4;-4) D(7; -1).
Viết phương trình của các đường thẳng AB, BC, CD và DA.
Phương trình của đường thẳng AB có dạng: y = ax + b.
Do phương trình đi qua A(4;5) và B(1; -1) nên ta có:
5 = a.4 + b (1)
-1 = a.1 + b (2)
Trừ từng vế của (1) và (2), ta có: 6 = 3a ⇒ a = 2.
Thay a = 2 và (1) để tìm b, ta có 5 = 2.4 + b ⇒ b = -3.
Vậy phương trình đường thẳng AB là: y = 2x – 3.
Làm tương tự như trên, ta có:
Phương trình đường thẳng BC là: y = -x.
Phương trình đường thẳng CD là: y = x – 8.
Phương trình đường thẳng DA là: y = -2x + 13.
Trên mặt phẳng tọa độ Oxy cho bốn điểm A, B, C, D có tọa độ nguyên như sau:
A(4;5) B(1;-1) C(4;-4) D(7; -1).
Tính (theo độ, phút) các góc của tứ giác ABCD bằng máy tính bỏ túi.
Hai đường chéo AC và BD vuông góc với nhau tại I.
- Đường thẳng AB có hệ số góc bằng 2, do đó ta có
tgα = 2 ⇒ α = 63 ° 26 ' (tính trên máy tính bỏ túi).
Suy ra ∠ (ABD) ≈ 63 ° 26 '
Tam giác ABD cân, nên cũng có ∠ (ADB) ≈ 63 ° 26 '
Từ đó suy ra ∠ (BAD) = 180 ° - 2. 63 ° 26 ' ≈ 53 ° 8 '
trong mặt phẳng hệ tọa độ oxy,cho điểm A(2;5)B(0;-7).tọa độ diểm M của AB là
Lời giải:
Tọa độ trung điểm $M$ của $AB$ là:
\(\left(\frac{x_A+x_B}{2}; \frac{y_A+y_B}{2}\right)=\left(\frac{2+0}{2}; \frac{5+(-7)}{2}\right)=(1;-1)\)
Trong mặt phẳng Oxy, cho bốn điểm \(A(2;1),B(1;4),C(4;5),D(5;2)\)
a) Chứng minh ABCD là một hình vuông
b) Tìm tọa độ tâm I của hình vuông ABCD
a) Ta có: \(\overrightarrow {AB} = ( - 1;3),\overrightarrow {BC} = (3;1),\overrightarrow {CD} = (1; - 3),\overrightarrow {DA} = ( - 3; - 1)\)
Suy ra \(AB = BC = CD = DA = \sqrt {10} \)
Mặt khác \(\overrightarrow {AB} .\overrightarrow {BC} = ( - 1).3 + 3.1 = 0 \Rightarrow AB \bot BC\)
Vậy ABCD là hình vuông
b) Ta có ABCD là hình vuông, nên tâm I là trung điểm của đoạn thẳng AC
Vậy tọa độ điểm I là \(I(3;3)\)

Trong mặt phẳng tọa độ cho Oxy bốn điểm A(3;-5), B(-3;3) ,C(-1;-2) ,D(5;-10). Hỏi G 1 3 ; - 3 là trọng tâm của tam giác nào dưới đây?
A. ABC.
B. BCD.
C. ACD.
D. ABD
Trong mặt phẳng tọa độ Oxy, cho điểm B(2;4). tìm tọa độ của điểm A biết V(O;2) (A)=B.
1.Trong mặt phẳng tọa độ Oxy cho hình bình hành ABCD với A (- 6;1); B (2;2) C (1;5) tọa độ đỉnh D là:
A. (5;2)
B. (-7;4)
C. (5;4)
D. (7;-4)
2.Trong mặt phẳng tọa độ Oxy cho tam giác ABC với A (- 1;3); B (2;1) C (5;5) tọa độ đỉnh D là của hình bình hành ABCD:
A. (0;4)
B. (8;1)
C. (8;3)
D. (-8;3)
Hướng dẫn em cách làm với ạ. Em cảm ơn nhiều.
1, Gọi tọa độ điểm D(x;y)
Ta có:\(\overrightarrow{AB}\left(8;1\right)\)
\(\overrightarrow{DC}\left(1-x;5-y\right)\)
Tứ giác ABCD là hình bình hành khi
\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow1-x=8;5-y=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=4\end{matrix}\right.\)
Vậy tọa độ điểm D(-7;4)
1. Trong mặt phẳng Oxy, có trọng tâm G(1,-1), M(2,1) và N(4,-2) lần lượt là trung điểm của AB, BC. Tìm tọa độ điểm B
2. Trong mặt phẳng Oxy, cho A(1,3), B(-2,2). Biết đường thẳng AB cắt trục tung tại điểm M(0,b). Giá trị b thuộc khoảng nào
3. Trong mặt phẳng tọa độ Oxy, cho A thỏa vecto OA= 2vecto i + 3vecto j. Tọa độ điểm A là
4. Trong mặt phẳng Oxy, cho vecto x=(1,2), vecto y=(3,4), vecto z=(5,-1). Tọa độ vecto u = 2vecto x + vecto y - vecto z là
5. Trong mặt phẳng tọa độ Oxy, cho M(2,-3), N(4,7). Tọa độ trung điểm I của đoạn thẳng MN là
6. Cho vecto x=(-4,7) và hai vecto a=(2,-1), b=(-3,4). Nếu vecto x = m vecto a + n vecto b thì m, n là cặp số nào