Số giao điểm của đồ thị hàm số y = x 3 - 4 x + 1 và đường thẳng y = x + 1 bằng:
A. 1
B. 2
C. 3
D. 4
Cho hàm số y=1/2 x^2 có đồ thị là (P) a) Vẽ đồ thị (P) của hàm số trên b) Tìm toạ độ giao điểm của (P) và đường thẳng (d) : y = x + 4
b: PTHĐGĐ là:
1/2x^2-x-4=0
=>x^2-2x-8=0
=>(x-4)(x+2)=0
=>x=4 hoặc x=-2
=>y=8 hoặc y=2
a: 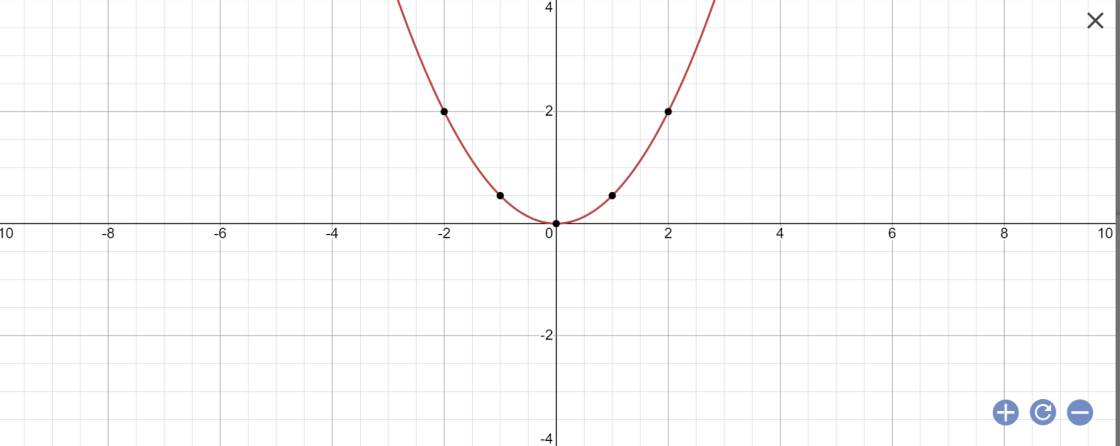
Tìm số giao điểm của đồ thị hàm số y = x/(x + 1) và đường thẳng y = -x.
A. 3
B. 1
C. 2.
D. 0
Đáp án C.
Phương trình hoành độ giao điểm x/(x + 1) = -x (DK: x ≠ -1)
⇔ x = -x2 – x
⇔ x2 + 2x = 0
⇔ ![]()
Cho hàm số: y = 2x + 3 (1)
1. Vẽ đồ thị hàm số (1) 2. Xác định m để đường thẳng (d): y = (2m – 1)x – 5m song song với đồ thị của hàm số (1). 3. Xác định m để đồ thị hàm số (1) và đường thẳng (d) cắt nhau tại một giao điểm có hoành độ dương.2) Để (d)//(1) thì \(\left\{{}\begin{matrix}2m-1=2\\-5m\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2m=3\\m\ne\dfrac{-3}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m\ne-\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow m=\dfrac{3}{2}\)
Vậy: Khi \(m=\dfrac{3}{2}\) thì (d)//(1)
Bài 1 :
1, Viết phương trình đường thẳng đi qua hai điểm (1;2) và (-1;-4)
2, Tìm tọa độ giao điểm của đường thẳng trên truc tung và trục hoành
Bài 2 : Cho hàm số y=(m-2)x+m+3
1, Tìm điều kiện của m để hàm số luôn nghịch biến
2, Tìm m để đồ thị hàm số cắt trục tung tại điểm có hoành độ bằng 3
3, Tìm m để đồ thị hàm số trên và các đồ thị của các hàm số y=-x+2 ; y=2x-1 đồng quy
Tìm số giao điểm của đồ thị hàm số y = x 4 − 4 + 5 và đường thẳng y = x
A. 3
B. 0
C. 2
D. 1
Đáp án B.
Phương trình hoành độ giao điểm là:
x 2 − 4 + 5 = x ⇔ x 2 − 4 = x − 5 ⇒ x ≥ 5
Bình phương 2 vế: x 2 − 4 = x 2 − 10 x + 25 ⇔ x = 29 10 (loại).
Tung độ giao điểm của đồ thị hàm số y = 2 x − 3 x + 3 và đường thẳng y = x − 1 là:
A. -3
B. 3.
C. -1
D. 0.
Đáp án C
PT hoành độ giao điểm là:
2 x − 3 x + 3 = x − 1 ⇔ x ≠ 1 2 x − 3 = x 2 + 2 x − 3 ⇔ x = 0 ⇒ y = − 1.
Tìm số giao điểm của đồ thị hàm số y = x 3 - 3 x + 3 và đường thẳng y= x.
A. 1
B. 2
C. 3
D. 0
Cho hàm số y = x 3 - 3 x 2 + 3 có đồ thị (C) và đường thẳng d : y = x + 3 . Số giao điểm của đường thẳng d với đồ thị (C) bằng bao nhiêu?
A. 0.
B. 2.
C. 1.
D. 3.
Tìm số giao điểm của đồ thị hàm số y = x + 2 x − 1 và đường thẳng y = 2 x .
A. 2
B. 0
C. 1
D. 3
Đáp án A
Số giao điểm của đồ thị hàm số y = x + 2 x − 1 và đường thẳng y = 2 x là số nghiệm của PT x + 2 x − 1 = 2 x ⇔ x 2 − x − 2 = 0 x ≠ 1 ⇔ x = − 1 x = 2
=> Có hai giao điểm.
Tìm số giao điểm của đồ thị hàm số y = x + 2 x - 1 và đường thẳng y = 2x
A. 1
B. 0
C. 3
D. 2
Đáp án D
Phương pháp:
Số giao điểm của hai đồ thị hàm số bằng số nghiệm của phương trình hoành đồ giao điểm của hai hàm số đó.
Cách giải:
Xét phương trình hoành độ giao điểm:
![]()
![]()
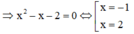
⇒ Số giao điểm của hai đồ thị hàm số là 2.