dùng Pitago đảo thử từng cặp 1 thôi:v

ta có: \(\left(b-c\right)^2+h^2=b^2+c^2-2bc+h^2\)(1)

vì tam giác ABC vuông ở A có đường cao AH nên \(a^2=b^2+c^2\)và\(AB.AB=AH.BC=2S\)hay\(b.c=a.h\)

\(\Rightarrow b^2+c^2-2bc+h^2=a^2-2ah+h^2=\left(a-h\right)^2\)

dể

\(AB^2=\left(1+1\right)^2+\left(2-0\right)^2=8\)

\(AC^2=\left(5+1\right)^2+\left(-2-0\right)^2=39\)

\(BC^2=\left(5-1\right)^2+\left(-2-2\right)^2=32\)

Cạnh lớn nhất là AC, ta có:

AC² < AB² + BC²

=> Tam giác ABC nhọn

Diện tích ABC= dt(CDEF) - dt(CDB) - dt(CFA) - dt(ABE) 

                     = 5.4 - 4.4/2 - 5.1/2 - 3.1/2

                      = 8

Gọi H(x,y), ta có BH vuông góc với AC => \(\overrightarrow{BH}.\overrightarrow{AC}=0\) => (x - 1).(5-0) + (y - 2)(-2 +1) = 0

=> 5x - y = 3    (1)

Phương trình đt AC là: \(\frac{y+1}{-2+1}=\frac{x-0}{5-0}\) => 5y + x = -5

Vì H thuộc AC nên  5y + x = -5    (2)

Từ (1) và (2), giải hệ pt ta có: x =5/13 và y = -14/13

Vậy H(5/13; -14/13)

AB2=(1+1)2+(2−0)2=8

AC2=(5+1)2+(−2−0)2=39

BC2=(5−1)2+(−2−2)2=32

Cạnh lớn nhất là AC, ta có:

AC2 < AB2 + BC2

=> Tam giác ABC nhọn

Diện tích ABC= dt(CDEF) - dt(CDB) - dt(CFA) - dt(ABE) 

                     = 5.4 - 4.4/2 - 5.1/2 - 3.1/2

                      = 8

Gọi H(x,y), ta có BH vuông góc với AC => BH−→−−.AC−→−−=0 => (x - 1).(5-0) + (y - 2)(-2 +1) = 0

=> 5x - y = 3    (1)

Phương trình đt AC là: y+1−2+1=x−05−0 => 5y + x = -5

Vì H thuộc AC nên  5y + x = -5    (2)

Từ (1) và (2), giải hệ pt ta có: x =5/13 và y = -14/13

Vậy H(5/13; -14/13)

5/13;-14/13

a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có

BE chung

góc ABE=góc HBE

=>ΔBAE=ΔBHE

b: Xét ΔEBC có góc EBC=góc ECB

nên ΔEBC cân tại E

mà EH là đường cao

nên H là trung điểm của BC

=>HB=HC

d: Xét ΔEAI vuông tại A và ΔEHC vuông tại H có

EA=EH

góc AEI=góc HEC

=>ΔEAI=ΔEHC

=>EI=EC>EH

a: A(3;1); B(2;6); C(4;-1)

\(AB=\sqrt{\left(2-3\right)^2+\left(6-1\right)^2}=\sqrt{5^2+1^2}=\sqrt{26}\)

\(AC=\sqrt{\left(4-3\right)^2+\left(-1-1\right)^2}=\sqrt{2^2+1^2}=\sqrt{5}\)

\(BC=\sqrt{\left(4-2\right)^2+\left(-1-6\right)^2}=\sqrt{2^2+7^2}=\sqrt{53}\)

Chu vi tam giác ABC là:

\(C_{ABC}=\sqrt{26}+\sqrt{5}+\sqrt{53}\left(đvđd\right)\)

b: Xét ΔABC có 

\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{26+5-53}{2\cdot\sqrt{26\cdot5}}\simeq-0,96\)

=>\(\widehat{A}\simeq165^0\)

c: Gọi H(x,y) là trực tâm của ΔABC

\(\overrightarrow{AH}=\left(x-3;y-1\right)\)

\(\overrightarrow{BH}=\left(x-2;y-6\right)\)

\(\overrightarrow{BC}=\left(2;-7\right);\overrightarrow{AC}=\left(1;-2\right)\)

H là trực tâm nên ta có: AH\(\perp\)BC và BH\(\perp\)AC

=>\(\left\{{}\begin{matrix}\overrightarrow{AH}\cdot\overrightarrow{BC}=0\\\overrightarrow{BH}\cdot\overrightarrow{AC}=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2\left(x-3\right)+\left(-7\right)\left(y-1\right)=0\\1\left(x-2\right)+\left(-2\right)\left(y-6\right)=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x-6-7y+7=0\\x-2-2y+12=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-7y=-1\\x-2y=-10\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x-7y=-1\\2x-4y=-20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3y=-1+20=19\\x-2y=-10\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=-\dfrac{19}{3}\\x=-10+2y=-10-\dfrac{38}{3}=-\dfrac{68}{3}\end{matrix}\right.\)

a) Vì M đối xứng với H qua BC nên BC là đường trung trực của MH

Suy ra: BH=BM và CH=CM

Xét ΔBHC và ΔBMC có 

BH=BM(cmt)

CH=CM(cmt)

BC chung

Do đó: ΔBHC=ΔBMC(c-c-c)

a)

Nhận xét: H là một điểm nằm trong tam giác ABC.

b)

Nhận xét: H trùng với đỉnh A của tam giác ABC.

c)

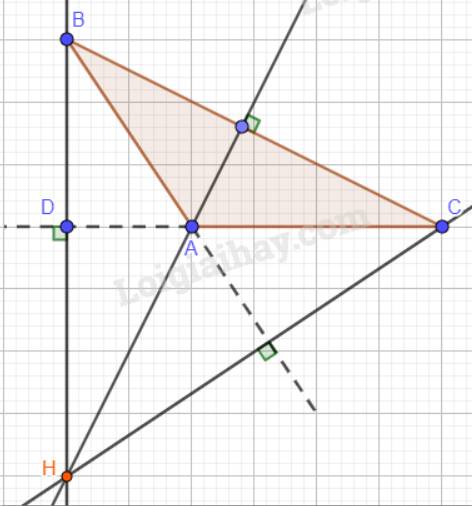
Nhận xét: H nằm ngoài tam giác ABC.

Ta có:

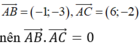
Suy ra tam giác ABC vuông tại A do đó trực tâm H trùng với A

Vậy H( -1 ; 3)

Chọn B.

Đáp án là A