Ta có: x - x 2 = x 1 - x

(Tử thức của phân thức bên phải bằng tử thức của phân thức bên trái chia cho (1 – x).

Do đó ta chia cả tử và mẫu của phân thức bên trái cho 1 – x thì thu được phân thức bên phải.)

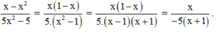
Vậy đa thức cần điền là -5x – 5.

mk mới hok lớp 6 thông cảm

3 y - x 2 = 3 . x - y 2 = x - y . 3 x - y

(Mẫu thức của phân thức bên trái bằng mẫu thức của phân thức bên phải chia cho 3(x – y)

Do đó ta chia cả tử và mẫu của phân thức bên phải cho 3(x – y) để thu được phân thức bên trái)

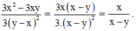
Vậy đa thức cần điền là x.

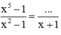
Ta để ý : x2 – 1 = (x – 1)(x + 1)

Do đó ta cần chia cả tử và mẫu của phân thức thứ nhất cho x – 1.

Mà ta có :

x5 – 1 = x5 – x4 + x4 – x3 + x3 – x2 + x2 – x + x – 1

= x4(x – 1) + x3(x – 1) + x2(x – 1) + x(x – 1) + (x – 1)

= (x – 1)(x4 + x3 + x2 + x + 1)

Do đó :

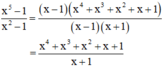
Vậy đa thức cần điền là x4 + x3 + x2 + x + 1.

\(\dfrac{2x}{x+1}=\dfrac{2x\cdot x}{x\left(x+1\right)}=\dfrac{2x^2}{x^2+x}\)

tính chất quan trọng phần thức với

\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow ad=bc\Rightarrow c=\dfrac{ad}{b}\)áp vào

\(\dfrac{x^5-1}{x^2-1}=\dfrac{A}{x+1}\Rightarrow A=\dfrac{\left(x^5-1\right)\left(x+1\right)}{x^2-1}\) {x khác +-1}

\(A=\dfrac{\left(x^5-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{\left[\left(x-1\right)\left(x^4+x^3+x^2+x+1\right)\right]\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\left(x^4+x^3+x^2+x+1\right)\)

Vậy đa thức cần điền là

\(A=\left(x^4+x^3+x^2+x+1\right)\)

Vế phải chứng tỏ đã chia mẫu của vế trái cho x - 1 ( vì x² – 1 = (x - 1)(x + 1)

Vậy phải chia tử của vế trái x⁵ – 1 cho x - 1

Vậy phải điền vào chỗ trống : x⁴ + x³ + x² + x + 1

x⁴ + x³ + x² + x +1

3 x 3 + 24 x = 3 x . x 2 + 8

(Tử thức của phân thức bên phải bằng tử thức của phân thức bên trái nhân với 3x.

Do đó ta nhân cả tử và mẫu của phân thức bên trái với 3x thì thu được phân thức bên phải)

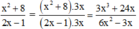
Vậy đa thức cần điền là 6 x 2 - 3 x