Để (d)//(d') thì m-2=-2

hay m=0

a: 

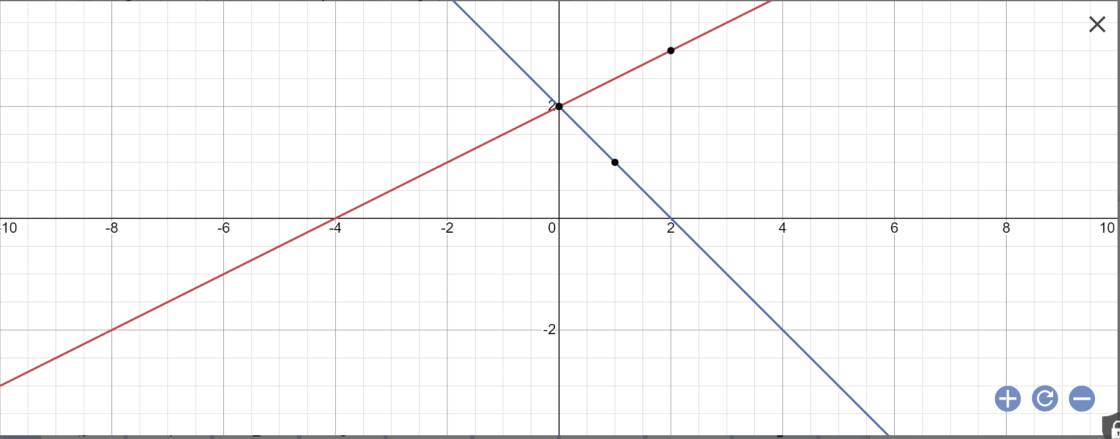
b: Gọi \(\alpha\) là góc tạo bởi (d1) với trục Ox

(d1): \(y=\dfrac{1}{2}x+2\)

=>\(a=\dfrac{1}{2}\)

=>\(tan\alpha=a=\dfrac{1}{2}\)

=>\(\alpha\simeq26^034'\)

c: Tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x+2=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{1}{2}x=-2\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=0\end{matrix}\right.\)

Tọa độ B là:

\(\left\{{}\begin{matrix}y=0\\-x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-x=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)

Tọa độ C là:

\(\left\{{}\begin{matrix}\dfrac{1}{2}x+2=-x+2\\y=-x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{2}x=0\\y=-x+2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=0\\y=-0+2=2\end{matrix}\right.\)

Vậy: A(-4;0); B(2;0); C(0;2)

\(AB=\sqrt{\left(2+4\right)^2+\left(0-0\right)^2}=6\)

\(AC=\sqrt{\left(0+4\right)^2+\left(2-0\right)^2}=\sqrt{4^2+2^2}=2\sqrt{5}\)

\(BC=\sqrt{\left(0-2\right)^2+\left(2-0\right)^2}=\sqrt{2^2+2^2}=2\sqrt{2}\)

Chu vi tam giác ABC là:

\(C_{ABC}=AB+AC+BC=6+2\sqrt{5}+2\sqrt{2}\)(cm)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{36+20-8}{2\cdot6\cdot2\sqrt{5}}=\dfrac{48}{24\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)

=>\(sinBAC=\sqrt{1-cos^2BAC}=\dfrac{1}{\sqrt{5}}\)

Diện tích tam giác ABC là:

\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)

\(=\dfrac{1}{2}\cdot6\cdot2\sqrt{5}\cdot\dfrac{1}{\sqrt{5}}=6\)

a: Tạo độ A là:

\(\left\{{}\begin{matrix}y=0\\-x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-x=-2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)

Tọa độ B là:

\(\left\{{}\begin{matrix}x=0\\y=-0+2=2\end{matrix}\right.\)

Vậy: O(0;0); A(2;0); B(0;2)

\(OA=\sqrt{\left(2-0\right)^2+\left(0-0\right)^2}=\sqrt{2^2}=2\)

\(OB=\sqrt{\left(0-0\right)^2+\left(2-0\right)^2}=\sqrt{2^2}=2\)

b: \(AB=\sqrt{\left(0-2\right)^2+\left(2-0\right)^2}=\sqrt{2^2+2^2}=2\sqrt{2}\)

Chu vi tam giác OAB là:

\(C_{OAB}=OA+OB+AB=4+2\sqrt{2}\)

Ta có: Ox\(\perp\)Oy

=>OA\(\perp\)OB

=>ΔOAB vuông tại O

=>\(S_{OAB}=\dfrac{1}{2}\cdot AO\cdot OB=\dfrac{1}{2}\cdot2\cdot2=2\)

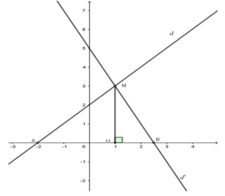
Xét phương trình hoành độ giao điểm của  d 1   v à   d 2

x   +   2   =   − 2 x   +   5 ⇔     x   =   1   ⇒   y   =   3   ⇒   d 1   ∩   d 2   t ạ i   M   ( 1 ;   3 )

Gọi H là chân đường vuông góc kẻ từ M tới Ox. Suy ra MH = 3

d ∩  Ox tại A (−2; 0) ⇒  OA = 2

d’ ∩  Ox tại B 5 2 ; 0   ⇒     O B   =     5 2

  A B   =   O A   +   O B   =   2   + 5 2   =     9 2

SMAB = 1 2  AB.MH = .  1 2 . 3 9 2 =   27 4 (đvdt)

Đáp án cần chọn là: D

\(y=\left(m-1\right)^2+2\left(d\right)\)

a) (d) đi qua A(1; 1)

\(\Rightarrow\)x=1; y=1

Thay x=1; y=1 vào (d)

\(\Rightarrow\) \(\left(m-1\right)^2\times1+2=1\)

\(\Leftrightarrow\left(m-1\right)^2=-1\)(vô lí)

Vậy ko có m để (d) đi qua A(1; 1)