Với giá trị nào của m thì hệ phương trình m x + y = 2 m x + m y = m + 1 có vô số nghiệm.
A. m = 1
B. m = −1
C. m = ± 1
D. m ≠ ± 1
cho hệ phương trình mx -y =2m 4x - my=6+m Với giá trị nào của m thì hệ phương trình có duy nhất một nghiệm Với giá trị nào của m thì hệ phương trình có vô số nghiệm Với giá trị nào của m thì hệ phương trình vô nghiệm
a: Để hệ có duy nhất 1 nghiệm thì \(\dfrac{m}{4}< >\dfrac{-1}{-m}=\dfrac{1}{m}\)
=>m^2<>4
=>m<>2 và m<>-2
b: Để hệ có vô số nghiệm thì \(\dfrac{m}{4}=\dfrac{-1}{-m}=\dfrac{2m}{m+6}=\dfrac{1}{m}\)
=>m^2=4 và 2m^2=m+6
=>m=2
c: Để hệ vô nghiệm thì m/4=1/m<>2m/m+6
=>m=-2
Cho hệ pt: \(\left\{{}\begin{matrix}3x-y=2\\9x-my=m\end{matrix}\right.\)
1. Với giá trị nào của m thì hệ phương trình vô nghiệm
2. Với giá trị nào của m thì hệ phương trình có vô số nghiệm?
3. Với giá trị nào của m thì hệ phương trình có nghiệm duy nhất
4. Tìm m để hệ có nghiệm duy nhất x> 0; y<0
cho hệ phương trình x-y+m=0 và (x+y-2)(x-2y+1) với giá trị nào của m thì hệ phương trình có một nghiệm duy nhất
Giúp mình với làm thiếu câu 1 cũng đc mình đang cần gấp (*/ω\*)
Cho hệ phương trình:
mx + y = 1
x + my = m + 1
a) Với giá trị nào của m thì hệ phương trình có nghiệm duy nhất
b) Với giá trị nào của m thì hệ phương có vô số nghiệm
c) Với giá trị nào của m thì hệ phương trình vô nghiệm
a) \(\left\{{}\begin{matrix}mx+y=1.\\x+my=m+1.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1-mx.\\x+m\left(1-mx\right)=m+1.\left(1\right)\end{matrix}\right.\)
Xét (1): \(x+m\left(1-mx\right)=m+1.\Leftrightarrow x+m-m^2x-m-1=0.\Leftrightarrow\left(1-m^2\right)x-1=0.\left(2\right)\)
Để hệ phương trình có nghiệm duy nhất. \(\Leftrightarrow\) (2) có nghiệm duy nhất.
\(\Leftrightarrow1-m^2\ne0.\Leftrightarrow m^2\ne1.\Leftrightarrow m\ne\pm1.\)
b) Để hệ phương trình có vô số nghiệm. \(\Leftrightarrow\) (2) có vô số nghiệm.
\(\Leftrightarrow\left\{{}\begin{matrix}1-m^2=0.\\-1=0.\end{matrix}\right.\) (vô lý).
\(\Rightarrow m\in\phi\).
c) Để hệ phương trình có vô nghiệm. \(\Leftrightarrow\) (2) có vô nghiệm.
\(\Leftrightarrow\left\{{}\begin{matrix}1-m^2=0.\\-1\ne0.\end{matrix}\right.\)\(\Leftrightarrow1-m^2=0.\Leftrightarrow m^2=1.\Leftrightarrow m=\pm1.\)
Với giá trị nào của m thì hệ phương trình : x - y = 2 4 5 x + 1 2 y = m + 1 nhận (3; 1) là nghiệm:
A. m = 1 2
B. m = 19 10
C. m = 3 10
D. Không có giá trị của m
Đáp án B
Nhận thấy 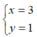 thỏa mãn : x - y = 2 nên ta thay
thỏa mãn : x - y = 2 nên ta thay 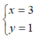 vào phương trình
vào phương trình
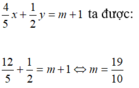
Với giá trị nào của m thì hệ phương trình
{(m+1)x - y = m+1
{x + (m+1)y = 2
Có nghiệm thoả mãn điều kiện S=x+y đạt giá trị nhỏ nhất
1.Cho hpt \(\hept{\begin{cases}nx-y=4\\x+y=1\end{cases}}\)
a) Với giá trị nào của n thì hệ phương trình có duy nhất nghiệm?
b) Với giá trị nào của n thì hệ phương trình vô nghiệm
Bài 3: Cho hệ phương trình \(\hept{\begin{cases}3x+my=4\\x+y=1\end{cases}}\)
a. Tìm m để hệ phương trình trên có nghiệm duy nhất, vô số nghiệm
b. Tìm m để hệ phương trình trên có nghiệm x<0, y>0
1:
a)\(\hept{\begin{cases}nx+x=5
\\x+y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x.\left(n+1\right)=5\left(1\right)\\x+y=1\end{cases}}\)
Cho hệ phương trình \(\hept{\begin{cases}mx-y=5\\x+y=1\end{cases}}\)
Với giá trị nào của m thì hệ phương trình có nghiệm duy nhất? Hệ phương trình vô nghiệm?
\(\hept{\begin{cases}mx-y=5\\x+y=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=1-x\\mx-1+x=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=1-x\\\left(m+1\right)x=6\end{cases}}\)
Để hệ có nghiệm duy nhất thì
m + 1 ≠ 0 <=> m ≠ - 1
Để hệ vô nghiệm thì
m + 1 = 0 <=> m = - 1
\(D=m+1\) ; \(D_x=5+1=6\) ; \(D_y=m-5\)
Để hpt có nghiệm duy nhất thì \(D\ne0\Rightarrow m\ne-1\)
Để hpt vô nghiệm thì \(\hept{\begin{cases}D=0\\D_x\ne0\end{cases}}\) hoặc \(\hept{\begin{cases}D=0\\D_y\ne0\end{cases}}\)
Dễ thấy ngay \(D_x\ne0\) . Vậy m = -1 thì hệ vô nghiệm.
Cho hệ phương trình 2x + y = 3 và 3x+2y= m (m là tham số)
a) Chứng tỏ rằng hệ phương trình luôn có một nghiệm duy nhất với mọi m. tìm nghiệm đó
b) với giá trị nào của m thì hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x >0 và y>0 (x=6-m; y=2m-9)