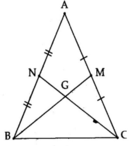
Cho tam giác ABC cân tại A có đường trung tuyến BM và CN.Chứng minh rằng BM=CN

Những câu hỏi liên quan
Cho tam giác ABC cân tại A vẽ hai đường trung tuyến BM và CN. Chứng minh rằng BM=CN
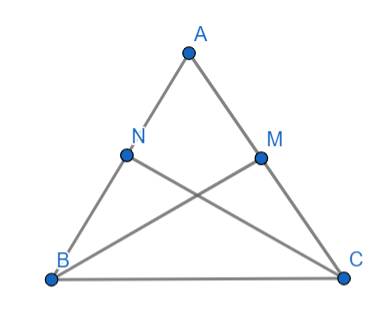
Xét △AMB và △ANC ta có:
AM=AN ( Vì M,N lần lượt là trung điểm của 2 cạnh AB, AC)
\(\widehat{A}\) là góc chung
AB=AC (Vì là hai cạnh bên trong tam giác cân)
\(\Rightarrow\Delta AMB=\Delta ANC\left(c-g-c\right)\)
\(\Rightarrow BM=CN\) (hai cạnh tương ứng)
Đúng 1
Bình luận (0)
Xét ΔAMB và ΔANC có
AM=AN
góc A chug
AB=AC
=>ΔAMB=ΔANC
=>BM=CN
Đúng 0
Bình luận (0)
Cho tam giác ABC có hai đường trung tuyến BM, CN.
a) Chứng minh nếu tam giác ABC cân tại A thì BM = CN.
b) Ngược lại nếu BM = CN, chứng minh:
i) GB = GC, GN = GM;
ii) BN = CM;
iii) tam giác ABC cân tại A.
Cho tam giác ABC cân tại A , các đường trung tuyến BM và CN cắt nhau tại G
Chứng minh tam giác ABC = tam giác ACN , từ đó suy ra BM=CN
Xét ΔABM và ΔACN có
AB=AC
góc BAM chung
AM=AN
=>ΔABM=ΔACN
=>BM=CN
Đúng 1
Bình luận (0)
Mình xin phép sửa đề:
Cho tam giác ABC cân tại A , các đường trung tuyến BM và CN cắt nhau tại G
Chứng minh tam giác ABN = tam giác ACN , từ đó suy ra BM=CN
`------`
\(\text{GT | AB = AC, }\widehat{\text{B}}=\widehat{\text{C}}\)
\(\text{CM | BM = CN}\)
\(\text{BM là đường trung tuyến}\)
`->`\(\text{MA = MC (1)}\)
\(\text{CN là đường trung tuyến}\)
`->`\(\text{NA = NB (2)}\)
`\Delta ABC` cân tại A
`->`\(\widehat{\text{B}}=\widehat{\text{C}}\text{, AB = AC (3)}\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\)
`->`\(\text{NA = NB = MA = MC}\)
Xét `\Delta ABM` và `\Delta ACN`:
\(\left\{{}\begin{matrix}\text{BM = CN}\\\widehat{\text{B}}=\widehat{\text{C}}\\\text{BC chung}\end{matrix}\right.\)
`=> \Delta ABM = \Delta ACN (c-g-c)`
`->`\(\text{BM = CN (2 cạnh tương ứng).}\)
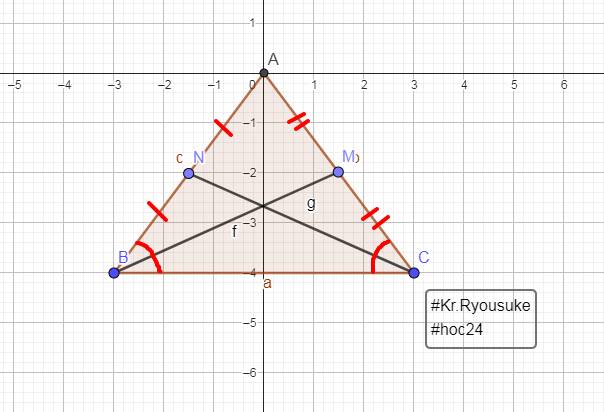
Đúng 1
Bình luận (7)
Cho tam giác ABC có đường trung tuyến BM bằng đường trung tuyến CN. Chứng minh rằng tam giác ABC cân.
Tham khảo:
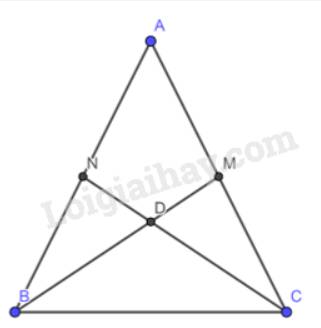
Gọi D là giao điểm của CN và BM
\( \Rightarrow \) D là trọng tâm tam giác ABC
\( \Rightarrow CD = \dfrac{2}{3}CN = BD = \dfrac{2}{3}BM\) ( do BM = CN )
\( \Rightarrow \) tam giác DBC cân tại D do BD = CD
\( \Rightarrow \) \(\widehat {DBC} = \widehat {DCB}\)(2 góc đáy trong tam giác cân) (1)
Xét \(\Delta NDB\) và \(\Delta MDC\) có :
BD = CD
\(\widehat {NDB} = \widehat {MDC}\) (2 góc đối đỉnh)
ND = DM (do cùng \( = \dfrac{1}{3}CN = \dfrac{1}{3}BM\) (tính chất của trung trực đi qua trọng tâm tam giác ))
\( \Rightarrow \Delta NDB=\Delta MDC\) (c.g.c)
\( \Rightarrow \,\widehat {NBD} = \widehat {MCD}\)(2 góc tương ứng) (2)
Từ (1) và (2) \( \Rightarrow \widehat {ABC} = \widehat {ACB}\) do \(\widehat {ABC} = \widehat {NBD} + \widehat {DBC}\) và \(\widehat {ACB} = \widehat {MCD} + \widehat {DCB}\)
\( \Rightarrow \Delta ABC\) cân tại A (do 2 góc bằng nhau)
Đúng 0
Bình luận (0)
Cho tam giác ABC có 2 đường trung tuyến BM và CN cắt nhau tại G
a) Chứng minh BM+CN>\(\dfrac{3}{2}\)BC
b) Biết BM=CN.Chứng minh rằng AG⊥BC
a: Xét ΔABC có
BM là đường trung tuyến
CN là đường trung tuyến
BM cắt CN tại G
DO đó:G là trọng tâm
=>BG=2/3BM; CG=2/3CN
\(BM+CN=\dfrac{2}{3}BG+\dfrac{2}{3}CG>\dfrac{2}{3}BC\)
b: BM=CN nên GB=GC
mà AB=AC
nên AG là đường trung trực của BC
=>AG\(\perp\)BC
Đúng 0
Bình luận (0)
cho tam giác abc có bc = 12, hai đường trung tuyến bm và cn cắt nhau tại g. chứng minh rằng: bm + cn > 18

BM = 3/2 BG, CN = 3/2 CG
Ta có BM + CN = 3/2 (BG + CG) > 3/2. BC = 3/2 x 12 = 18
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Vẽ BM và CN là 2 đường trung tuyến. a/ Chứng minh: BM = CN b/Chứng minh: Tứ giác BNMC là hình thang cân. c/ Gọi I là giao điểm của BM và CN. Chứng minh: AI vuông góc với MN
Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến.
a) Chứng minh rằng BM = CN
b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC
Tham khảo:
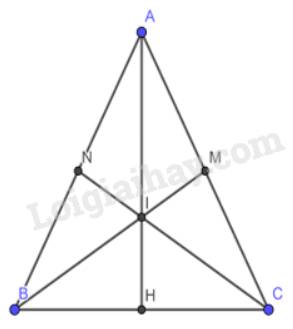
a) Vì tam giác ABC cân tại A theo giả thiết. BM và CN là 2 đường trung tuyến nên M, N là 2 trung điểm của AC, AB.
Vì AB = AC (tính chất tam giác cân)
\( \Rightarrow \dfrac{{AB}}{2} = \dfrac{{AC}}{2} = AN = AM\)
Xét tam giác AMB và tam giác ANC ta có :
AM = AN (cmt)
AB = AC
Góc A chung
\( \Rightarrow \Delta AMB =\Delta ANC\)
\( \Rightarrow BM = CN\) ( 2 cạnh tương ứng )
b) Vì BM và CN là các đường trung tuyến
Mà I là giao điểm của BM và CN
\( \Rightarrow \) I là trọng tâm của tam giác ABC
\( \Rightarrow \) AI là đường trung tuyến của tam giác ABC hay AH đường là trung tuyến của tam giác ABC
\( \Rightarrow \) H là trung điểm của BC
Đúng 0
Bình luận (0)
Cho tam giác ABC có 2 đường trung tuyến BM, CN cắt nahu tại điểm G.
a, C/m nếu tam giác ABC cân tại A thì BM = CN.
b, Ngược lại nếu BM = CN , c/m:
i,GB = GC, GN = GM;
ii, BN = CM
iii, Tam giác ABC cân tại A