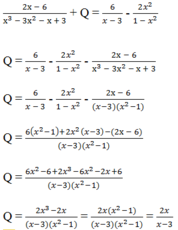x + 2 . P x 2 - 1 = x - 2 . Q x 2 - 2 x + 1

⇒ x + 2 . P . x 2 - 2 x + 1 = x 2 - 1 x - 2 . Q

Hay  x + 2 x - 1 2 . P = x - 1 x + 1 x - 2 . Q

Chọn P = (x – 2)(x + 1) =  x 2 - x - 2  thì Q = (x + 2)(x – 1) = x 2 + x - 2

x + 2 P x - 2 = x - 1 Q x 2 - 4

⇒ x + 2 . P . x 2 - 4 = x - 2 x - 1 . Q

Hay (x + 2)(x – 2)(x + 2).P = (x – 2)(x – 1).Q

Chọn P = (x – 1) thì Q = x + 2 2

Ta có: \(C=\dfrac{2x+1}{x^2+x-2}=\dfrac{2x+1}{\left(x-1\right)\left(x+2\right)}\)

ĐKXĐ: \(\left\{{}\begin{matrix}x\ne1\\x\ne-2\end{matrix}\right.\) 

\(\left|2x+5\right|=7\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+5=7\left(x\ge-\dfrac{5}{2}\right)\\2x+5=-7\left(x< -\dfrac{5}{2}\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=2\\2x=-12\end{matrix}\right.\) 

\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(ktm\right)\\x=-6\left(tm\right)\end{matrix}\right.\)

Thay x=-6 vào C ta có:

\(C=\dfrac{2\cdot-6+1}{\left(-6\right)^2+\left(-6\right)-2}=\dfrac{-12+1}{36-6-2}=\dfrac{-11}{28}\)

a) \(\dfrac{\left(x+2\right)P}{x-2}=\dfrac{\left(x-1\right)Q}{x^2-4}\)

\(\Leftrightarrow\left(x^2-4\right)\left(x+2\right)P=\left(x-2\right)\left(x-1\right)Q\)

\(\Leftrightarrow\)\(\left(x+2\right)^2\left(x-2\right)P=\left(x-2\right)\left(x-1\right)Q\)

\(\Leftrightarrow\)\(\left(x+2\right)^2P=\left(x-1\right)Q\)

\(\Leftrightarrow P=x-1\)

\(Q=\left(x+2\right)^2=x^2+4x+4\)

b)\(\dfrac{\left(x+2\right)P}{x^2-1}=\dfrac{\left(x-2\right)Q}{x^2-2x+1}\)

\(\Leftrightarrow\left(x-1\right)^2\left(x+2\right)P=\left(x+1\right)\left(x-1\right)\left(x-2\right)Q\)

\(\Leftrightarrow\left(x-1\right)\left(x+2\right)P=\left(x+1\right)\left(x-2\right)Q\)

\(\Leftrightarrow P=\left(x+1\right)\left(x-2\right)=x^2-x-2\)

\(Q=\left(x-1\right)\left(x+2\right)=x^2+x-2\)

Ta có

Thay x = 1/2 : \(f\left(\frac{1}{2}\right)+3f\left(2\right)=\frac{1}{4}\)

Thay x = 2: \(f\left(2\right)+3f\left(\frac{1}{2}\right)=4\)

\(\Rightarrow\left[f\left(2\right)+3f\left(\frac{1}{2}\right)\right]-3\left[f\left(\frac{1}{2}\right)+3f\left(2\right)\right]=4-\frac{3}{4}\)

\(\Rightarrow-5f\left(2\right)=\frac{13}{4}\Leftrightarrow f\left(2\right)=-\frac{13}{20}\)

Ta có :

Thay x = 1/2 : ƒ (12 )+3ƒ (2)=14 

Thay x = 2: ƒ (2)+3ƒ (12 )=4

⇒[ƒ (2)+3ƒ (12 )]−3[ƒ (12 )+3ƒ (2)]=4−34 

thanks

sdjhshj

\(A=\dfrac{1}{x^2+y^2}+\dfrac{1}{xy}=\left(\dfrac{1}{x^2+y^2}+\dfrac{1}{2xy}\right)+\dfrac{1}{2xy}\)

Áp dụng BĐT Schwarz : \(\dfrac{1}{x^2+y^2}+\dfrac{1}{2xy}\ge\dfrac{\left(1+1\right)^2}{x^2+y^2+2xy}=\dfrac{4}{\left(x+y\right)^2}=4\)

Lại có \(\dfrac{1}{2xy}=\dfrac{2}{4xy}\ge\dfrac{2}{\left(x+y\right)^2}=2\)

Cộng vế với vế được P \(\ge6\) ("=" khi x = y = 1/2)

Vậy Min P = 6 <=> x = y = 1/2