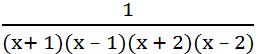Đố em tìm được giá trị của x để giá trị của phân thức 4 x 2 - 4 x 3 + x 4 x 3 - 2 x 2 bằng: 0

Những câu hỏi liên quan
Đố em tìm được giá trị của x để giá trị của phân thức
4
x
2
-
4
x
3
+
x
4
x
3
-
2
x
2
bằn...
Đọc tiếp
Đố em tìm được giá trị của x để giá trị của phân thức 4 x 2 - 4 x 3 + x 4 x 3 - 2 x 2 bằng: 2
Điều kiện: x 3 - 2 x 2 = x 2 x - 2 ≠ 0 ⇒ x ≠ 0 và x ≠ 2
Ta có: 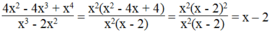
Nếu phân thức đã cho bằng 2 thì biểu thức x - 2 cũng có giá trị bằng 2. Suy ra: x- 2 = 2 ⇒ x = 4. Với x = 4 thỏa mãn điều kiện.
Vậy khi x = 4 thì phân thức có giá trị bằng 2.
Đúng 0
Bình luận (0)
Đố em tìm được giá trị của x để giá trị của phân thức
4
x
2
-
4
x
3
+
x
4
x
3
-
2
x
2
bằn...
Đọc tiếp
Đố em tìm được giá trị của x để giá trị của phân thức 4 x 2 - 4 x 3 + x 4 x 3 - 2 x 2 bằng: – 2
Điều kiện: x 3 - 2 x 2 = x 2 x - 2 ≠ 0 ⇒ x ≠ 0 và x ≠ 2
Ta có: 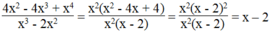
Nếu phân thức đã cho bằng -2 thì biểu thức x - 2 cũng có giá trị bằng -2. Suy ra: x - 2 = -2 ⇒ x = 0 không thỏa mãn điều kiện.
Vậy không có giá trị nào của x để phân thức bằng -2
Đúng 0
Bình luận (0)
Cho phân thức : x ^ 2 +4 X+4 phần x +2
a) Với điều kiện nào của x thì giá trị của phân thức được xác định
b) Rút gọn phân thức
c) Tìm giá trị của x để giá trị của phân thức bằng 1
d) Có giá trị của x để giá trị của phân thức bằng 0 hay không
Bài 2: (3 điểm) Cho phân thức \(\dfrac{4x-4}{2x^2-2}\)
a/ Tìm điều kiện của x để giá trị của phân thức được xác định.
b/ Tìm giá trị của x để phân thức có giá trị bằng –2 .
c/ Tìm giá trị của x để phân thức có giá trị là số nguyên.
a) ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
b) Ta có: \(\dfrac{4x-4}{2x^2-2}\)
\(=\dfrac{4\left(x-1\right)}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{2}{x+1}\)
Để phân thức có giá trị bằng -2 thì \(\dfrac{2}{x+1}=-2\)
\(\Leftrightarrow x+1=-1\)
hay x=-2(thỏa ĐK)
Đúng 0
Bình luận (0)
Bài 9: Cho biểu thức: [(4/x-4)-(4/x-4)].(x^2+8x+16/32) a) Tìm điều kiện của x để phân thức xác định?b) Tìm giá trị của x để phân thức có giá trị bằng 1/3 c) Tìm giá trị của x để phân thức có giá trị bằng 1d) Tìm giá trị nguyên của x để phân thức có giá trị nguyên?e) Tìm giá trị của x để phân thức luôn dương?
Đọc tiếp
Bài 9: Cho biểu thức: [(4/x-4)-(4/x-4)].(x^2+8x+16/32)
a) Tìm điều kiện của x để phân thức xác định?
b) Tìm giá trị của x để phân thức có giá trị bằng 1/3
c) Tìm giá trị của x để phân thức có giá trị bằng 1
d) Tìm giá trị nguyên của x để phân thức có giá trị nguyên?
e) Tìm giá trị của x để phân thức luôn dương?
Đố. Đố em tìm được phân thức (của một biến x) mà giá trị của nó được xác định với mọi giá trị của x khác các ước của 2.
Các ước của 2 là ±1, ±2.
Vậy phân thức cần tìm phải xác định với mọi x ≠ ±1; ±2.
Ta có thể chọn:
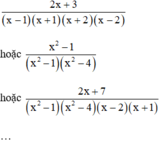
Có rất nhiều đáp án khác.
Đúng 0
Bình luận (0)
Đố :
Đố em tìm được một cặp phân thức của biến x mà giá trị của phân thức này bằng 0 thì giá trị của phân thức kia không xác định và ngược lại khi giá trị của phân thức kia bằng 0 thì giá trị của phân thức này không xác định.
Em có thể tìm được bao nhiêu cặp phân thức như thế ?
1.Cho biểu thức C x³/x²-4 - x/x-2 - 2/x+2 a,tìm giá trị của biến để biểu thức được xác địnhb,Tìm x để C0c,Tìm giá trị nguyên của x để C nhận giá trị dương 2,cho P (2+x/2-x + 4x²/x²-4 - 2-x/2+x): x²-3x/2x²-x³a,Tìm điều kiện của x để giá trị của P được xác định B, rút gọn Pc,Tính giá trị P với |x-5|2d,Tìm x để P03,cho biểu thức B [x+1/2x-2 + 3/x²-1 - x+3/2x+2]. 4x²-4/5a,Tìm điều kiện của x để giá trị biểu thức được xác định b,CMR khi giá trị của biểu thức không phụ thuộc vào giá trị của biến x?...
Đọc tiếp
1.Cho biểu thức C = x³/x²-4 - x/x-2 - 2/x+2
a,tìm giá trị của biến để biểu thức được xác định
b,Tìm x để C=0
c,Tìm giá trị nguyên của x để C nhận giá trị dương
2,cho P = (2+x/2-x + 4x²/x²-4 - 2-x/2+x): x²-3x/2x²-x³
a,Tìm điều kiện của x để giá trị của P được xác định
B, rút gọn P
c,Tính giá trị P với |x-5|=2
d,Tìm x để P<0
3,cho biểu thức B = [x+1/2x-2 + 3/x²-1 - x+3/2x+2]. 4x²-4/5
a,Tìm điều kiện của x để giá trị biểu thức được xác định
b,CMR khi giá trị của biểu thức không phụ thuộc vào giá trị của biến x?
4,Cho phân thức C = 3x²-x/9x²-6x+1
a, tìm điều kiện xác định phân thức
b,tính giá trị phân thức tại x=-8
c,Tìm x để giá trị của phân thức nhận giá trị dương
1.a)\(\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}\)
\(=\frac{x^3}{\left(x+2\right)\left(x-2\right)}-\frac{x}{x-2}-\frac{2}{x+2}\)
Để biểu thức được xác định thì:\(\left(x+2\right)\left(x-2\right)\ne0\)\(\Rightarrow x\ne\pm2\)
\(\left(x+2\right)\ne0\Rightarrow x\ne-2\)
\(\left(x-2\right)\ne0\Rightarrow x\ne2\)
Vậy để biểu thức xác định thì : \(x\ne\pm2\)
b) để C=0 thì ....
Đúng 1
Bình luận (0)
1, c , bn Nguyễn Hữu Triết chưa lm xong
ta có : \(/x-5/=2\)
\(\Rightarrow\orbr{\begin{cases}x-5=2\\x-5=-2\end{cases}}\Rightarrow\orbr{\begin{cases}x=7\\x=3\end{cases}}\)
thay x = 7 vào biểu thứcC
\(\Rightarrow C=\frac{4.7^2\left(2-7\right)}{\left(7-3\right)\left(2+7\right)}=\frac{-988}{36}=\frac{-247}{9}\)KL :>...
thay x = 3 vào C
\(\Rightarrow C=\frac{4.3^2\left(2-3\right)}{\left(3-3\right)\left(3+7\right)}\)
=> ko tìm đc giá trị C tại x = 3
Đúng 0
Bình luận (0)
chết mk nhìn nhầm phần c bài 2 :
\(2,\left(\frac{2+x}{2-x}+\frac{4x^2}{x^2-4}-\frac{2-x}{2+x}\right):\frac{x^2-3x}{2x^2-x^3}\)
Để P xác định
\(\Rightarrow2-x\ne0\Rightarrow x\ne2\)
\(2+x\ne0\Rightarrow x\ne-2\)
\(x^2-4\ne0\Rightarrow x\ne0\)
\(x^2-3x\ne0\Rightarrow x\ne3\)
b, \(P=\left(\frac{2+x}{2-x}+\frac{4x^2}{\left(2+x\right)\left(2-x\right)}+\frac{2-x}{2+x}\right):\frac{x\left(x-3\right)}{x^2\left(2-x\right)}\)
\(P=\left[\frac{4+4x+x^2}{\left(2-x\right)\left(2+x\right)}-\frac{4x^2}{\left(2+x\right)\left(2-x\right)}-\frac{4-4x+x^2}{\left(2+x\right)\left(2-x\right)}\right].\frac{x\left(2-x\right)}{x-3}\)
\(P=\left[\frac{8x-4x^2}{\left(2-x\right)\left(2+x\right)}\right].\frac{x\left(2-x\right)}{x-3}=\frac{4x\left(2-x\right)}{\left(2-x\right)\left(2+x\right)}.\frac{x\left(2-x\right)}{x-3}\)
\(P=\frac{4x^2\left(2-x\right)}{\left(x-3\right)\left(2+x\right)}\)
d, ĐỂ \(p=\frac{8x^2-4x^3}{x^2-x-6}< 0\)
\(TH1:8x^2-4x^3< 0\)
\(\Rightarrow8x^2< 4x^3\)
\(\Rightarrow2< x\Rightarrow x>2\)
\(TH2:x^2-x-6< 0\Rightarrow x^2< x+6\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Đố :
Đố em tìm được một phân thức (của một biến x) mà giá trị của nó được xác định với mọi giá trị của x khác các ước của 2 ?
Các ước của 2 là: 1;−1;2;−2. Do đó, mẫu của phân thức cần tìm là:
(x+1)(x−1)(x+2)(x−2)≠0
Vậy có thể chọn phân thức