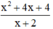Question

Bài 9: Cho biểu thức: [(4/x-4)-(4/x-4)].(x^2+8x+16/32)

a) Tìm điều kiện của x để phân thức xác định?

b) Tìm giá trị của x để phân thức có giá trị bằng 1/3

c) Tìm giá trị của x để phân thức có giá trị bằng 1

d) Tìm giá trị nguyên của x để phân thức có giá trị nguyên?

e) Tìm giá trị của x để phân thức luôn dương?

Answer 1

Sửa đề: \(\left\lbrack\frac{4}{x-4}-\frac{4}{x+4}\right\rbrack\cdot\frac{x^2+8x+16}{32}\)

Đặt \(A=\left\lbrack\frac{4}{x-4}-\frac{4}{x+4}\right\rbrack\cdot\frac{x^2+8x+16}{32}\)

a: ĐKXĐ: x∉{4;-4}

b: \(A=\left\lbrack\frac{4}{x-4}-\frac{4}{x+4}\right\rbrack\cdot\frac{x^2+8x+16}{32}\)

\(=\frac{4\left(x+4\right)-4\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}\cdot\frac{\left(x+4\right)^2}{32}\)

\(=\frac{4x+16-4x+16}{x-4}\cdot\frac{x+4}{32}=\frac{32}{x-4}\cdot\frac{x+4}{32}=\frac{x+4}{x-4}\)

\(A=\frac13\)

=>\(\frac{x+4}{x-4}=\frac13\)

=>3(x+4)=x-4

=>3x+12=x-4

=>2x=-16

=>x=-8(nhận)

c: A=1

=>x+4=x-4

=>4=-4(loại)

=>x∈∅

d: Để A nguyên thì x+4⋮x-4

=>x-4+8⋮x-4

=>8⋮x-4

=>x-4∈{1;-1;2;-2;4;-4;8;-8}

=>x∈{5;3;6;2;8;0;12;-4}

Kết hợp ĐKXĐ, ta được: x∈{5;3;6;2;8;0;12}

e: Để A>0 thì \(\frac{x+4}{x-4}>0\)

=>x-4>0 hoặc x+4<0

=>x>4 hoặc x<-4