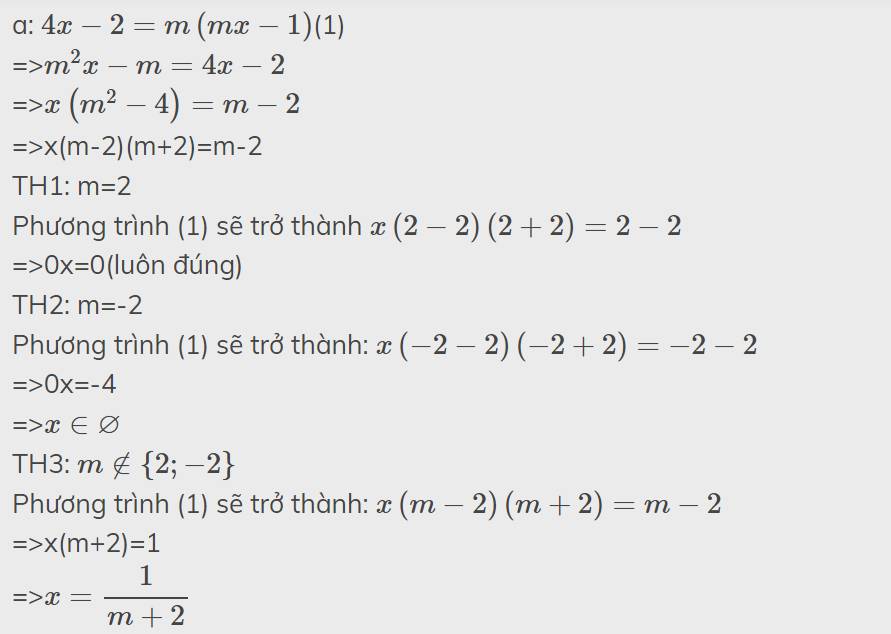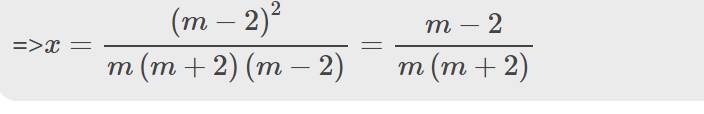Giải và biện luận các phương trình sau theo tham số m: m2x + 6 = 4x + 3m

Những câu hỏi liên quan
Giải và biện luận các phương trình sau theo tham số m
2 m x - 2 + 4 = 3 - m 2 x
Phương trình đã cho tương đương với phương trình
(m - 1)(m + 3)x = 4(m - 1)
Với m ≠ 1 và m ≠ -3 phương trình có nghiệm ![]()
Với m = 1 mọi số thực x đều là nghiệm của phương trình;
Với m = -3 phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Giải và biện luận các phương trình sau theo tham số m
a) m(x - 2) = 3x + 1;
b) m2x + 6 = 4x + 3m;
c) (2m + 1)x – 2m = 3x – 2.
a) ⇔ (m – 3)x = 2m + 1.
Nếu m ≠ 3 phương trình có nghiệm duy nhất x = .
Nếu m = 3 phương trình trở thành 0x = 7. Vô nghiệm.
b) ⇔ (m2 – 4)x = 3m – 6.
Nếu m2 – 4 ≠ 0 ⇔ m ≠ ± 2, có nghiệm x = .
Nếu m = 2, phương trình trở thành 0x = 0, mọi x ∈ R đều nghiệm đúng phương trình.
Nếu m = -2, phương trình trở thành 0x = -12. Vô nghiệm.
c) ⇔ 2(m – 1)x = 2(m-1).
Nếu m ≠ 1 có nghiệm duy nhất x = 1.
Đúng 1
Bình luận (0)
Giải và biện luận các phương trình sau theo tham số m.
2 x - 5 m = 2 x - 3 m

Kết luận:
Với m > 0 phương trình có nghiệm là x = 2m.
Với m = 0 phương trình có nghiệm là mọi số thực không âm.
Với m < 0 phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Giải và biện luận theo tham số m các phương trình sau
4 x - 2 2 x - 1 = m - 1
Điều kiện của phương trình là m > 1/2
Với điều kiện đó vế trái dương, nên vế phải cũng dương nên m > 1. Lúc đó ta có:
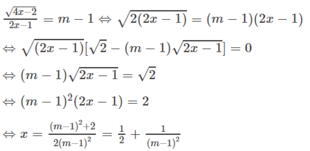
Giá trị ![]() thỏa mãn điều kiện x > 1/2
thỏa mãn điều kiện x > 1/2
Kết luận. Với m ≤ 1 phương trình vô nghiệm.
Với m > 1 nghiệm của phương trình là
![]()
Đúng 0
Bình luận (0)
Giải và biện luận các phương trình sau theo tham số m.
3 x + 4 m = 4 x - 7 m
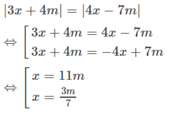
Vậy phương trình đã cho có hai nghiệm x = 11m và x = 3m/7 với mọi giá trị của m.
Đúng 0
Bình luận (0)
Cho phương trình
m
2
x
-
6
4
x
-
3
m
Trong các kết luận sau, kết luận nào sai? A. Khi
m
-
2
, phương trình đã cho vô nghiệm; B. Khi
m
-
2
, phương trình...
Đọc tiếp
Cho phương trình m 2 x - 6 = 4 x - 3 m
Trong các kết luận sau, kết luận nào sai?
A. Khi m = - 2 , phương trình đã cho vô nghiệm;
B. Khi m = - 2 , phương trình đã cho có nghiệm duy nhất;
C. Khi m = 2 , phương trình đã cho có tập nghiệm là ;
D. Khi m ≠ ± 2 , phương trình đã cho có hai nghiệm phân biệt.
Giải và biện luận các phương trình sau theo tham số m :
a. \(m\left(x-2\right)=3x+1\)
b. \(m^2x+6=4x+3m\)
c. \(\left(2m+1\right)x-2m=3x-2\)
a) ⇔ (m – 3)x = 2m + 1.
Nếu m ≠ 3 phương trình có nghiệm duy nhất x =b) ⇔ (m2 – 4)x = 3m – 6.
Nếu m2 – 4 ≠ 0 ⇔ m ≠ ± 2, có nghiệm x =c) ⇔ 2(m – 1)x = 2(m-1).
Nếu m ≠ 1 có nghiệm duy nhất x = 1. Nếu m = 1 mọi x ∈ R đều là nghiệm của phương trình.
Đúng 0
Bình luận (0)
Cho phương trình m 2 x + 6 = 4 x + 3 m . Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm.
A. m = 2.
B. m ≠ −2.
C. m ≠ −2 và m ≠ 2.
D. m ∈ R.
Phương trình viết lại m 2 - 4 x = 3 m - 6
Phương trình đã cho vô nghiệm khi m 2 − 4 = 0 3 m − 6 ≠ 0 ⇔ m = ± 2 m ≠ 2 ⇔ m = − 2
Do đó, phương trình đã cho có nghiệm khi m ≠ −2.
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Giải và biện luận các phương trình sau
a) 4x-2=m(mx-1)
f) m2x-3=4x-(m-1)
g)m3x-4=m2+4mx-4m