Cho tam giác ABC có a 2 = b 2 + c 2 + 2 b c . Số đo của góc A là
A. 135 °
B. 45 °
C. 120 °
D. 150 °
Câu 1:Cho tam giác ABC có góc B lớn hơn góc A là 15°,góc C lơn hơn góc A là 45°. Tính số đo góc B và A của tam giác ABC
Câu 2:Cho tam giác ABC có B lớn hơn A là 24°,góc C nhỏ hơn góc A là 30°. Tính số đo góc A và C của tam giác ABC
Câu 3:Cho tam giác ABC có góc B nhỏ hơn góc A là 25°,góc C lớn hơn góc B là 35°. Tính số đo góc B và C của tam giác ABC
Câu 4:Cho tam giác có góc A=30°. Kẻ các tia phân giác ED và CE của góc B và góc C. Biết số đo AEC bằng số đo góc ADB. Tính số đo góc B và C của tam giác ABC
câu 5:Cho tam giác ABC và một D thuộc miền trong tam giác.CMR: Góc BAC nhỏ hơn góc BDC
Cho tam giác ABC có số đo 3 góc là A, B, C thỏa mãn điều kiện \(\tan\dfrac{A}{2}+\tan\dfrac{B}{2}+\tan\dfrac{C}{2}=\sqrt{3}\) . Tam giác ABC là tam giác gì ?
\(\dfrac{A}{2}+\dfrac{B}{2}=\dfrac{\pi}{2}-\dfrac{C}{2}\Rightarrow tan\left(\dfrac{A}{2}+\dfrac{B}{2}\right)=tan\left(\dfrac{\pi}{2}-\dfrac{C}{2}\right)\)
\(\Rightarrow\dfrac{tan\dfrac{A}{2}+tan\dfrac{B}{2}}{1-tan\dfrac{A}{2}tan\dfrac{B}{2}}=cot\dfrac{C}{2}=\dfrac{1}{tan\dfrac{C}{2}}\)
\(\Rightarrow tan\dfrac{A}{2}.tan\dfrac{C}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}=1-tan\dfrac{A}{2}tan\dfrac{B}{2}\)
\(\Rightarrow tan\dfrac{A}{2}tan\dfrac{B}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}+tan\dfrac{C}{2}tan\dfrac{A}{2}=1\)
Ta có:
\(tan\dfrac{A}{2}+tan\dfrac{B}{2}+tan\dfrac{C}{2}\ge\sqrt{3\left(tan\dfrac{A}{2}tan\dfrac{B}{2}+tan\dfrac{B}{2}tan\dfrac{C}{2}+tan\dfrac{C}{2}tan\dfrac{A}{2}\right)}=\sqrt{3}\)
Dấu "=" xảy ra khi và chỉ khi \(A=B=C\) hay tam giác ABC đều
Cho tam giác ABC có a = 2, b = 3, c = 19 . Số đo của góc C là
A. 135 °
B. 150 °
C. 60 °
D. 120 °
Áp dụng hệ quả định lí cosin trong tam giác ta có:
cos C = 2 2 + 3 2 − 19 2 2.2.3 = 13 − 19 12 = − 1 2 ⇒ C ^ = 120 °
Chọn D
bài 2 cho tam giác ABC có A= B+C. Hai đường phân giác của góc C cắt nhau tại D a, tính số đo góc A b, tính số đo góc BOC
a: góc A=180/2=90 độ
b: góc OBC+góc OCB=90/2=45 độ
=>góc BOC=135 độ
a. Cho tam giác ABC vuông góc tại A. I là giao điểm của các tia phân giác của hai góc đỉnh B và C.tính số đo góc BIC
b. cho tam giác ABC có góc A=a(0 mũ 0 <a<180 độ).I là giao điểm của các tia phân giác của hai góc B và C .Tính số đo góc BIC theo a .Tìm a, biết BIC =2 góc BAC
1. Cho tam giác ABC có góc A bằng 74 độ góc B bằng 47 độ. Tính số đo góc ngoài tại đỉnh C?
2. Cho tam giác DEF có góc F bằng 40 độ, D - E bằng 52 độ. Tính số đo góc D, góc E?
3. Cho tam giác ABC có góc A bằng x, số đo góc B bằng 2x, số đo góc C bằng 3x. Tính số đo các góc của tam giác ABC
Bài 1:
Số đo góc ngoài tại đỉnh C là \(74^0+47^0=121^0\)
Câu 2:
Đặt \(\widehat{D}=a;\widehat{E}=b\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=52\\a+b=140\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=96\\b=44\end{matrix}\right.\)
Bài 3:
Theo đề, ta có: x+2x+3x=180
=>6x=180
=>x=30
=>\(\widehat{A}=30^0;\widehat{B}=60^0;\widehat{C}=90^0\)
Cho Tam giác ABC có góc A = góc B + 2 góc C và độ dài 3 cạnh của tam giác là 3 số tự nhiên liên tiếp.
a) Tính độ dài các cạnh của tam giác.
b) Tính số đo của góc A.
Cho tam giác ABC có BC = a, AC = b, AB = c. Tính số đo góc A, biết b(b^2 - a^2) = c.(a^2 - c^2).
Cho tam giác ABC, biết rằng số đo các góc A ^ , B ^ , C ^ tỉ lệ với 2, 3, 4. Số đo của góc A là:
A. 20 °
B. 40 °
C. 60 °
D. 80 °

Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
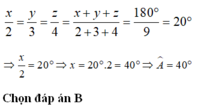
1,cho tam giác ABC có góc A=90 độ, góc C=40 độ, vẽ đường phân giác AD và đường cao AH. Tính số đo góc HAD
2, cho tam giác ABC có góc B>góc C, vẽ phân giác AD của góc A
a, c/m góc ADC-ADB=B-C
b, dường thẳng chứa tia phân giác góc ngoài đỉnh A của tam giác ABC cắt đường thẳng BC tại E, C/m góc AEB=(B-C):2
3, cho tam giác ABC biết góc A=70 độ, B-C=30 độ
c/m tam giác ABC có 2 góc bằng nhau
4, cho tam giác ABC biết C=1/3.B, B=1/2.A
LÀm đc bài nào làm giúp mk nhé! cần gấp lắm! làm hết càng tốt, mk kick cho