giúp tớ tớ cần gấp 

Những câu hỏi liên quan
Các bạn ơi , giúp tớ 2 bài này với ạ , tớ đang cần gấp gấp lắm cho nên mong các bạn giúp tớ tối nay tớ phải nộp rồi , tớ cảm ơn
Tìm x xong rồi tìm y
3 thì làm kiểu gì cũng được
Đúng 0
Bình luận (0)
Bài 3:
Hình 1:
Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(x+60^0+40^0=180^0\)
=>\(x=180^0-100^0=80^0\)
Hình 2:
Xét ΔABD có \(\widehat{ADC}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADC}=\widehat{ABD}+\widehat{BAD}=110^0\)
=>\(y=110^0\)
ΔDAC cân tại D
=>\(\widehat{DAC}=\widehat{DCA}=\dfrac{180^0-\widehat{ADC}}{2}\)
=>\(x=\dfrac{180^0-110^0}{2}=35^0\)
Hình 3:
Ta có: \(\widehat{CAB}+60^0=180^0\)
=>\(\widehat{CAB}=180^0-60^0=120^0\)
Xét ΔCAB có \(\widehat{CAB}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(x+2x+120^0=180^0\)
=>\(3x=60^0\)
=>\(x=20^0\)
Hình 4:
Ta có: \(\widehat{ADC}+\widehat{ADB}=180^0\)
=>\(\widehat{ADB}=180^0-80^0=100^0\)
Xét ΔADB có
\(\widehat{ADB}+\widehat{ABD}+\widehat{BAD}=180^0\)
=>\(x+60^0+100^0=180^0\)
=>\(x=20^0\)
ta có: \(\widehat{ACD}+135^0=180^0\)
=>\(\widehat{ACD}=180^0-135^0=45^0\)
Xét ΔACD có \(\widehat{ACD}+\widehat{ADC}+\widehat{DAC}=180^0\)
=>\(y+80^0+45^0=180^0\)
=>\(y=55^0\)
Đúng 1
Bình luận (0)
giúp tớ tớ cần gấp 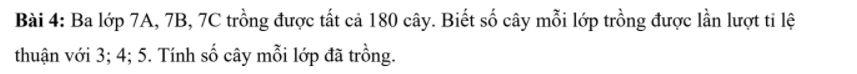
Gọi số cây lớp 7A,7B,7C lần lượt là a,b,c(cây;a,b,c∈N*)
Áp dụng tc dtsbn:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{180}{12}=15\\ \Leftrightarrow\left\{{}\begin{matrix}a=45\\b=60\\c=75\end{matrix}\right.\)
Vậy ...
Đúng 0
Bình luận (1)
 giúp tớ tớ cần gấp
giúp tớ tớ cần gấp
giúp tớ,tớ cần gấp
giúp tớ tớ cần gấp
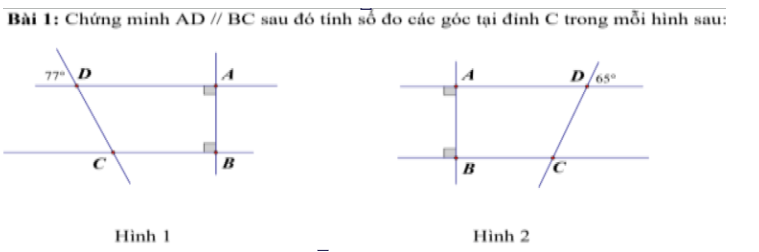
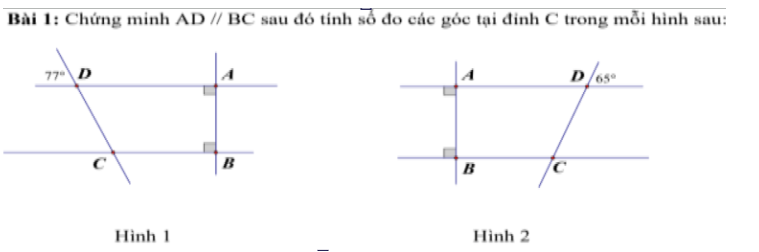
Hình 1:
Ta có: AD\(\perp\)AB
CB\(\perp\)AB
Do đó: AD//CB
Hình 2:
Ta có: \(AD\perp AB\)
BC\(\perp\)AB
Do đó: AD//BC
Đúng 0
Bình luận (0)
Ta có :
\(A\perp D;A\perp B;B\perp C\)
\(\Rightarrow\)AD//CB
\(\widehat{C1}=\widehat{D1}\) (đồng vị)
\(\Rightarrow\widehat{C1}=77^o\)
\(\Rightarrow\widehat{C2}=180^o-77^o=103^o\) (trong cùng phía)
\(\widehat{C4}=\widehat{C2}\) (đối đỉnh)
\(\Rightarrow\widehat{C4}=103^o\)
\(\widehat{C3}=\widehat{C3}\) (đối đỉnh)
\(\Rightarrow\widehat{C3}=77^o\)
Đúng 0
Bình luận (1)
giúp tớ,tớ cần gấp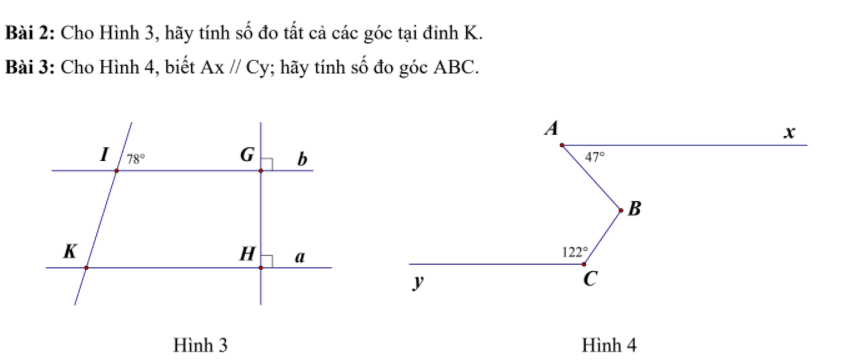
Bài 2:
Vì $b\perp GH, a\perp GH\Rightarrow a\parallel b$
Do đó:
$\widehat{K_1}=\widehat{I_1}=78^0$ (hai góc đồng vị)
$\widehat{K_2}=\widehat{K_1}=78^0$ (hai góc đối đỉnh)
$\widehat{K_4}=180^0-\widehat{K_1}=180^0-78^0=102^0$ (hai góc kề bù)
$\widehat{K_3}=\widehat{K_4}=102^0$ (đối đỉnh)
Đúng 0
Bình luận (0)
Bài 3: Kẻ tia $Bt\parallel Ax$. Vì $Ax\parallel Cy$ nên $Bt\parallel Cy$
Ta có:
$\widehat{B_1}=\widehat{BAx}=47^0$ (hai góc so le trong)
$\widehat{B_2}+\widehat{BCy}=180^0$ (trong cùng phía)
$\Rightarrow \widehat{B_2}=180^0-\widehat{BCy}=180^0-122^0=58^0$
Do đó: $\widehat{ABC}=\widehat{B_1}+\widehat{B_2}=47^0+58^0=105^0$
Đúng 0
Bình luận (0)
giúp tớ,tớ cần gấp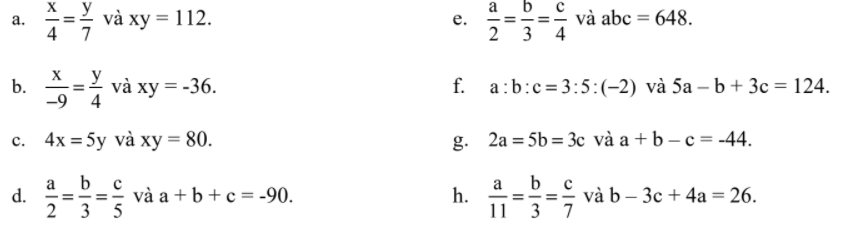
a, \(\dfrac{x}{4}=\dfrac{y}{7};xy=112\)
Ta có: \(\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{x.y}{4.7}=\dfrac{112}{28}=4\)
*\(\dfrac{x}{4}=4=>x=16\)
*\(\dfrac{y}{7}=4=>y=28\)
Vậy (x, y)\(\in\){ 16, 28}
Nhiều quá, nên tách ra nha
Đúng 1
Bình luận (0)
c, \(4x=5y;xy=80\)
= \(\dfrac{4x}{1}=\dfrac{5y}{1}=\dfrac{x}{\dfrac{1}{4}}=\dfrac{y}{\dfrac{1}{5}}=\dfrac{xy}{\dfrac{1}{4}.\dfrac{1}{5}}=\dfrac{80}{\dfrac{1}{20}}=1600\)
=> \(4x=1600=>x=400\)
\(5y=1600=>y=320\)
Vậy( x; y)∈{ 400; 320
Đúng 1
Bình luận (0)
e, \(\dfrac{x}{-9}=\dfrac{y}{4};xy=-36\)
Ta có: \(\dfrac{x}{-9}=\dfrac{y}{4}=\dfrac{xy}{\left(-9\right).4}=\dfrac{-36}{-36}=1\)
* \(\dfrac{x}{-9}=1=>x=-9\)
* \(\dfrac{y}{4}=1=>y=4\)
Vậy( x, y) ∈{ -9; 4}
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp tớ với,tớ cần gấp
Bài 7:
Ta có: \(\widehat{xOy}+\widehat{xOm}=180^0\)
\(\Leftrightarrow\widehat{xOm}=180^0-50^0\)
hay \(\widehat{xOm}=130^0\)
Đúng 2
Bình luận (0)
giúp tớ với,tớ cần gấp