Cho tam giác ABC vuông tại A, kẻ AH vuông góc BC. Tìm tam giác đồng dạng với tam giác ABC?
A. ΔHAC
B. ΔAHC
C. ΔAHB
D. ΔABH
Cho tam giác ABC cân tại A kẻ AH vuông góc với BC tại H
a/Chứng minh ΔAHB =ΔAHC. Từ đó suy ra HB=HC
b/Kẻ HD vuông góc với AB(D ϵ AB), HE vuông với AC (E ϵ AC). Chứng minh ΔHDE là tam giác cân
c/Chứng minh AD=AE và DC//BC
a.Xét tam giác vuông AHB và tam giác vuông AHC, có:
AB = AC ( ABC cân )
góc B = góc C ( ABC cân )
Vậy tam giác vuông AHB = tam giác vuông AHC ( cạnh huyền. góc nhọn)
=> HB = HC ( 2 cạnh tương ứng )
b.Xét tam giác vuông ADH và tam giác vuông AEH, có:
AH: cạnh chung
góc DAH = góc EAH ( AH là đường cao cũng là đường phân giác )
Vậy tam giác vuông ADH = tam giác vuông AEH
=> HD = HE ( 2 cạnh tương ứng )
=> tam giác HDE cân tại H
c.Xét tam giác vuông AEC và tam giác vuông ADB, có:
AB = AC ( ABC cân )
góc A: chung
Vậy tam giác vuông AEC = tam giác vuông ADB ( cạnh huyền.góc nhọn)
=> AD = AE ( 2 cạnh tương ứng )
=> tam giác ADE cân tại A
=> AH vuông với DE, mà AH cũng vuông với BC
=> DE//BC ( DE ko phải DC nha bạn )
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó:ΔAHB=ΔAHC
Suy ra: HB=HC
b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: HD=HE
hay ΔHDE cân tại H
c: Ta có: ΔADH=ΔAEH
nên AD=AE
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (hình 147). Chứng minh rằng ΔAHB =ΔAHC (giải bằng 2 cách)
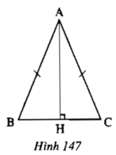
- Cách 1: ΔABC cân tại A nên ∠B = ∠C và AB = AC
Xét hai tam giác vuông ΔAHB và ΔAHC đều vuông tại H có:
AB = AC (GT)
∠B = ∠C
⇒ ΔAHB =ΔAHC (cạnh huyền – góc nhọn)
- Cách 2:
Xét hai tam giác vuông ΔAHB và ΔAHC đều vuông tại H có:
AB = AC
AH chung
⇒ ΔAHB = ΔAHC (cạnh huyền – cạnh góc vuông)
Cho tam giác ABC vuông tại A có AB = 6cm,AC= 8cm. Kẻ đường cao AH. (H thuộc BC)
a) chứng minh : tam giác ABC đồng dạng tam giác HBA
b) tính độ dài các cạnh BC, AH?,
c)kẻ HM vuông góc với AB,HN vuông góc với AC.chứng minh tam giác AMN dồng dạng với tam giác ACB
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: BC=10cm
AH=4,8cm
c: Xét ΔABH vuông tại H có HM là đườg cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔACH vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
hay AM/AC=AN/AB
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
AM/AC=AN/AB
Do đó: ΔAMN\(\sim\)ΔACB
\(a)\) Xét \(\Delta ABC\) và \(\Delta HBA:\)
\(\widehat{BAC}=\widehat{BHA}\left(=90^o\right).\\ \widehat{ABC}chung.\\ \Rightarrow\Delta ABC\sim\Delta HBA\left(g-g\right).\)
\(b)\) Xét \(\Delta ABC\) vuông tại A:
\(+)BC^2=AB^2+AC^2\left(Pytago\right).\\ \Rightarrow BC^2=6^2+8^2=36+64=100.\\ \Rightarrow BC=10\left(cm\right).\)\(+)AH.BC=AB.AC\) (Hệ thức lượng).\(\Rightarrow AH.10=6.8.\\ \Rightarrow AH=4,8\left(cm\right).\)\(c)\) Xét \(\Delta ABH\) vuông tại H, đường cao MH:\(AH^2=AM.AB\) (Hệ thức lượng). \(\left(1\right)\)Xét \(\Delta ACH\) vuông tại H, đường cao NH:\(AH^2=AN.AC\) (Hệ thức lượng). \(\left(2\right)\)Từ \(\left(1\right);\left(2\right)\Rightarrow AM.AB=AN.AC.\)Xét \(\Delta ACB\) và \(\Delta AMN:\)\(\Rightarrow\dfrac{AB}{AN}=\dfrac{AC}{AM}.\)\(\widehat{A}chung.\\ \dfrac{AB}{AN}=\dfrac{AC}{AM}\left(cmt\right).\\ \Rightarrow\Delta ACB\sim\Delta AMN\left(c-g-c\right).\)Cho tam giác ABC vuông tại A. Đường cao AH. a) Chứng minh rằng tam giác ABC đồng dạng với tam giác HBA. b) Chứng minh rằng tam giác ABC đồng dạng với tam giác HAC. c) AC^2 = BC.CH
đ) Trên HC lấy điểm D sao cho HD = HA. đường vuông góc với BC tại D cắt AC tại E. kẻ AG là đường phân giác của tam giác ABC
cm GB / BC = HD/(AH + HC)
cho tam giác ABC vuông tại A,có ab=9cm=,ac=12cm tia phân giác của góc a cắt BC tại D từ d kẻ DE vuông góc ac (e thuộc Ac)
a) so sách tỉ số BD/DC=AE/EC
b) kẻ AH vuông với BC C/minh tam giác HBA đồng dạng với tam giác EDC
a:
Ta có: DE\(\perp\)AC
AB\(\perp\)AC
Do đó: DE//AB
Xét ΔCAB có ED//AB
nên \(\dfrac{CE}{EA}=\dfrac{CD}{DB}\)
=>\(\dfrac{BD}{DC}=\dfrac{AE}{EC}\)
b: Xét ΔHBA vuông tại H và ΔEDC vuông tại E có
\(\widehat{EDC}=\widehat{HBA}\)(hai góc đồng vị, DE//AB)
Do đó: ΔHBA~ΔEDC
Cho tam giác ABC vuông tại A , biết AB=12cm , AC= 16cm kẻ AH vuông góc với BC ( H thuộc BC)
a. chứng minh tam giác ABC đồng dạng với tam giác HBA
b.tính BC, AH , HB
c. Kẻ đường phân giác BD , tính AD/CD
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: \(BC=\sqrt{AB^2+AC^2}=20\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\)
\(BH=\sqrt{12^2-9.6^2}=7.2\left(cm\right)\)
Cho tam giác ABC vuông tại A, AH vuông góc với CB a) Chứng minh tam giác ABC đồng dạng với tam giác HBA b) chứng minh tam giác ABC đồng dạng với tam giác HAC c) Kẻ phân giác BF, BF cắt AH tại K Chứng minh BH/BA = BK/BF
a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
b) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
Cho tam giác ABC vuông tại A, AH vuông góc BC tại H.
a) CM: tam giác AHC đồng dạng tam giác BAC
b) Kẻ phân giác CD của góc BCA. Kẻ AI vuông góc CD tại I. CMR: AI.CD=AC.AD
c) CMR: tam giác IHC đồng dạng tam giác BDC
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A,
D BC .
a). Tính DB/DC
b). Kẻ đường cao AH ( H BC ). Chứng minh rằng: ΔAHB đồng dạng ΔCHA .
| c).Tính tỷ số diện tích của tam giác AHB và CHA |
d) Chứng minh AD2 =AB.AC – DB.DC
giúp mik với ạaa