Tính tổng tất cả các giá trị nguyên của hàm số y = 3 sin x - c o sx - 4 2 sin x + c o sx - 3
A. 8
B. 5
C. 6
D. 9
Tính tổng tất cả các giá trị nguyên của hàm số y = 3 . sin x - cos x - 4 2 . sin x + cos x - 3
A. 8
B. 5
C. 6
D. 9
Tính tổng tất cả các giá trị nguyên của hàm số y = 2 sin x - cos x - 4 2 sin x + cos x - 3
A. 2
B. 8
C. 6
D. 5
Tính tổng tất cả các giá trị nguyên của hàm số y = 2 sin x - cos x - 4 2 sin x + cos x - 3
A. 3
B. 8
C. 6
D. 5
Tính tổng tất cả các giá trị nguyên của hàm số y = 3 sinx − cosx − 4 2 sinx + cosx − 3
A. 3
B. 6
C. 8
D. 5
Tính tổng tất cả các giá trị nguyên của hàm số y=\(\dfrac{3sinx-cosx-4}{2sinx+cosx-3}\)
\(y=\dfrac{3sinx-cosx-4}{2sinx+cosx-3} \Leftrightarrow (2sinx+cosx-3)y=3sinx-cosx-4 \Leftrightarrow (3-2y)sinx+(y-1)cosx=4-3y \)
\(\Rightarrow (3-2y)^2+(y-1)^2 ≥ (4-3y)^2 \Leftrightarrow 5y^2−14y+10 ≥ 16−24y+9y^2 \Leftrightarrow 1 ≤ y ≤ \dfrac{3}{2}\)
Vậy hàm số không có giá trị nguyên.
Gọi S là tập tất cả các giá trị nguyên của m để giá trị lớn nhất của hàm số y = sin x + m 3 - 2 sin x thuộc đoạn [-2;2]. Khi đó số phần tử của S là
A. 11
B. 10
C. Vô số
D. 9
Chọn A
Đặt ![]() ta có:
ta có: ![]()
Ta có 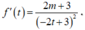
Do m ∈ Z nên ta xét hai trường hợp sau
+TH1: ![]() thì hàm số đồng biến trên [-1;1].
thì hàm số đồng biến trên [-1;1].
![]()
Xét ![]()
![]()
+TH2: ![]() thì hàm số nghịch biến trên [-1;1]
thì hàm số nghịch biến trên [-1;1]
![]()
Xét ![]()
Vậy ![]()
Vậy tập S có 4 phần tử.
Nên chọn A.
Nhận xét của Admin tổ 4:
Cách khác liên quan đến bản chất Max, Min của hàm số:
Để giá trị lớn nhất của hàm số y = sin x + m 3 - 2 sin x thuộc đoạn [-2;2]
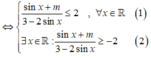
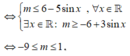
Cho hàm số y = f (x) có đồ thị như hình bên. Gọi S là tập tất cả các giá trị nguyên dương của tham số m để hàm số y = f x - 2018 + m có 5 điểm cực trị. Tổng tất cả các giá trị của tập S bằng
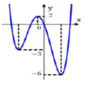
A. 9
B. 7
C. 12
D. 18
Cho hàm số y = 4 3 sin 3 x + 2 cos 2 x - ( 2 m 2 - 5 m + 2 ) sin x - 2017 Gọi S là tập hợp tất cả các giá trị nguyên của m sao cho hàm số đồng biến trên khoảng ( 0 ; π 2 ) Tìm số phần tử của S.
A. 0
B. 1
C. 2
D. Vô số
Đáp án B
Ta có y ' = 4 sin 2 x cos x sin x - ( 2 m 2 - 5 m + 2 ) cos x = cos x [ ( 2 sin x - 1 ) 2 - ( 2 m 2 - 5 m + 3 ) ]
Xét trên ( 0 ; π 2 ) ta thấy cos x > 0 , để hàm số đồng biến trên khoảng này thì ( 2 sin x - 1 ) 2 - ( 2 m 2 - 5 m + 3 ) ≥ 0 với ∀ x ∈ ( 0 ; π 2 ) hay ( 2 m 2 - 5 m + 3 ) ≤ 0 ⇒ 1 ≤ m ≤ 3 2 do m nguyên nên tồn tại duy nhất m=1
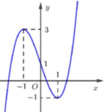
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ dưới. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(sin x) = 2sin x +m có nghiệm thuộc khoảng 0 ; π . Tổng các phần tử của S bằng:
A. -10
B. -8
C. -6
D. -5