Trong các hàm số f 1 x = s inx , f 2 x = x + 1 , f 3 x = x 3 − 3 x và f 4 x = x + x − 1 k h i x ≥ 1 2 − x k h i x < 1 có tất cả bao nhiêu hàm số là hàm liên tục trên ℝ ?
A. 1
B. 2
C. 4
D. 3
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x 2 - 1 ) ( x - 2 ) . Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số f ( x 2 + m ) có 5 điểm cực trị. Số phần tử của tập S là.
A. 4
B. 1
C. 3
D. 2
Cho các Hàm số f1(x) = 5x2; f2(x) = -6x; f3(x) = 7/x; f4(x) = x5; f5(x) = x6 + x4. Trong các hàm số trên, hàm số nào có tính chất f(x) = f(-x) với mọi x?
cho hàm số f1(x)=x; f2(x)=-2x; f3(x)=1; f4(x) =5; f5(x) =\(\frac{1}{x}\); f6(x) = x2. Trong các hàm số trên, hàm số nào có tính chất f(-x)=f(x); f(-x)=-f(x); f(x1+x2)=f(x1)+f(x2); f(x1.x2)=f(x1).f(x2)
Cho các hàm số f1(x)=\(\frac{1}{x}\);f2(x)=x2. Chứng tỏ trong các hàm số trên có tính chất
f(x1.x2)=f(x1).f(x2)
Cho hàm số f(x) có đạo hàm không âm trên [0;1] thỏa mãn ( [ f ( x ) ] 2 [ f ' ( x ) ] 2 ) e 2 x = 1 + [ f ( x ) ] 2 và f(x)> 0 với ∀x∈[0;1], biết f(0)=1. hãy chọn khẳng định đúng trong các khẳng định sau
A. 5 2 <f(1)< 3
B. 3<f(1)< 7 2
C. 2<f(1)< 5 2
D. 3 2 <f(1)< 2
Cho hàm số y=f(x) có đạo hàm trên R thỏa mãn f(-1)= f(3)= 0 và đồ thị hàm số y=f' (x) có dạng như hình vẽ. Hàm số y= [ f ( x ) ] 2 nghịch biến trên khoảng nào trong các khoảng sau?
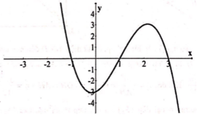
A. (-2;1).
B. (1;2).
C. (0;4).
D. (-2;2).
Cho hàm số y = f(x) có đạo hàm f'(x) = (x2-1)(x2-x-2). Hỏi hàm số g(x) = f(x-x2) đồng biến trên khoảng nào trong các khoảng sau?
A. (-1;1)
B. (0;2)
C. (-∞;-1)
D. (2;+∞)
\(f'\left(x\right)=\left(x-1\right)\left(x+1\right)\left(x+1\right)\left(x-2\right)=\left(x+1\right)^2\left(x-1\right)\left(x-2\right)\)
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\) (chỉ quan tâm nghiệm bội lẻ)
\(g'\left(x\right)=\left(1-2x\right)f'\left(x-x^2\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\f'\left(x-x^2\right)=0\end{matrix}\right.\)
\(f'\left(x-x^2\right)=0\Rightarrow\left[{}\begin{matrix}x-x^2=1\\x-x^2=2\end{matrix}\right.\) (đều vô nghiệm)
\(\Rightarrow g\left(x\right)\) đồng biến khi \(x< \dfrac{1}{2}\) và nghịch biến khi \(x>\dfrac{1}{2}\)
\(\Rightarrow C\) đúng (do \(\left(-\infty;-1\right)\subset\left(-\infty;\dfrac{1}{2}\right)\)
Cho hàm số f(x) có đạo hàm không âm trên [0;1] thỏa mãn [ f ( x ) ] 4 . [ f ' ( x ) ] 2 ( x 2 + 1 ) = 1 + f 3 ( x ) và f(x)>0 biết f(0) = 2 Hãy chọn khẳng định đúng trong các khẳng định sau:
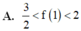
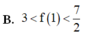
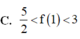
Cho hàm số y= f(x). Đồ thị hàm số y= f’(x) như hình dưới và f(-2) = f( 2) = 0
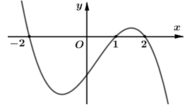
Hàm số g( x) = [ f( 3-x)]2 nghịch biến trên khoảng nào trong các khoảng sau?
A. (- 2; -1)
B. (1; 2)
C. (2; 5)
D. ( 5 ; + ∞ )
Cho các hàm số f1(x)=x, f2(x)=-2x, f3(x)=1, f4(x)=5, f5(x)=1/x, f6(x)=x2. Trong các hàm số trên, hàm số nào có tính chất f(-x)=f(x), f(-x)=-f(x), f(x1+x2)=f(x1)+f(x2), f(x1.x2)=f(x1).f(x2) ?