Tìm tất cả các nguyên hàm của hàm số f x = c o s 2 x là:
A. sin 2 x + C .
B. 1 2 sin 2 x + C .
C. − 1 2 sin 2 x + C .
D. 2 sin 2 x + C .
Cho hàm số y = 4 3 sin 3 x + 2 cos 2 x - ( 2 m 2 - 5 m + 2 ) sin x - 2017 Gọi S là tập hợp tất cả các giá trị nguyên của m sao cho hàm số đồng biến trên khoảng ( 0 ; π 2 ) Tìm số phần tử của S.
A. 0
B. 1
C. 2
D. Vô số
Đáp án B
Ta có y ' = 4 sin 2 x cos x sin x - ( 2 m 2 - 5 m + 2 ) cos x = cos x [ ( 2 sin x - 1 ) 2 - ( 2 m 2 - 5 m + 3 ) ]
Xét trên ( 0 ; π 2 ) ta thấy cos x > 0 , để hàm số đồng biến trên khoảng này thì ( 2 sin x - 1 ) 2 - ( 2 m 2 - 5 m + 3 ) ≥ 0 với ∀ x ∈ ( 0 ; π 2 ) hay ( 2 m 2 - 5 m + 3 ) ≤ 0 ⇒ 1 ≤ m ≤ 3 2 do m nguyên nên tồn tại duy nhất m=1
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x 2 - 1 ) ( x - 2 ) . Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số f ( x 2 + m ) có 5 điểm cực trị. Số phần tử của tập S là.
A. 4
B. 1
C. 3
D. 2
Cho hàm số \(y=f\left(x\right)\) liên tục trên R, có đạo hàm \(f'\left(x\right)=x\left(x-1\right)^2\left(x-2\right)\) . Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho hàm số \(y=f\left(\dfrac{x+2}{x+m}\right)\) đồng biến trên khoảng \(\left(10;+\infty\right)\) . Tính tổng các phần tử của S.
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ dưới. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(sin x) = 2sin x +m có nghiệm thuộc khoảng 0 ; π . Tổng các phần tử của S bằng:
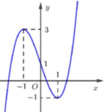
A. -10
B. -8
C. -6
D. -5
Cho hàm số f(x) thỏa mãn f x + f ' x = e - x , ∀ x ∈ ℝ và f(0) = 2. Tất cả các nguyên hàm của f x e 2 x là
A. x - 2 e x + e x + C
B. x + 2 e x + e x + C
C. x - 1 e x + C
D. x + 1 e x + C
Cho hàm số f(x) thỏa mãn f x + f ' x = e - x và f(0) = 2. Tất cả các nguyên hàm của f x e 2 x là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số f(x) liên tục trên R. Biết x.ex là 1 nguyên hàm của f(x).e2x, tìm họ tất cả nguyên hàm của hàm số f'(x).e2x
Từ giả thiết: \(\int f\left(x\right).e^{2x}dx=x.e^x+C\)
Đạo hàm 2 vế:
\(\Rightarrow f\left(x\right).e^{2x}=e^x+x.e^x\)
\(\Rightarrow f\left(x\right)=\dfrac{e^x+x.e^x}{e^{2x}}=\dfrac{x+1}{e^x}\)
Xét \(I=\int f'\left(x\right)e^{2x}dx\)
Đặt \(\left\{{}\begin{matrix}u=e^{2x}\\dv=f'\left(x\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2.e^{2x}dx\\v=f\left(x\right)\end{matrix}\right.\)
\(\Rightarrow I=f\left(x\right).e^{2x}-2\int f\left(x\right).e^{2x}dx=\left(\dfrac{x+1}{e^x}\right)e^{2x}-2.x.e^x+C\)
\(=\left(1-x\right)e^x+C\)
Tìm nguyên hàm của hàm số f ( x ) = ( sin x + c o s x ) 2
A. ∫ f ( x ) d x = x + 1 2 c o s 2 x + C
B. ∫ f ( x ) d x = 1 2 c o s 2 x + C
C. ∫ f ( x ) d x = - 1 2 c o s 2 x + C
D. ∫ f ( x ) d x = x - 1 2 c o s 2 x + C
Cho hàm số f(x)=(2 x +m)/(√x+1) với m là tham số thực, m>1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là
A. 1
B. 3
C. 0
D. 2
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình vẽ

Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m sao cho hàm số y=f(x+m-3) nghịch biến trên khoảng (-2;4). Số phần tử của S là? biết m ϵ [-1;5)